Autor: Admin

Categorías
Modelo Lineal General Temas Básicos

Asunción de normalidad

Asunciones: Normalidad

En esta entrada se recoge una breve explicación de la tan aclamada asunción de normalidad, haciendo hincapié en a que se refiere realmente dicha asunción, si es o no relevante, que implicaciones tiene su incumplimiento y como "evaluarla" y tomar decisiones en investigación para el análisis de datos.

Dentro de los análisis clásicos paramétricos para variables cuantitativas que asumiremos continuas, tales como una t-Student, un Análisis de la Varianza (ANOVA) o covarianza (ANCOVA), o lo que es lo mismo, el modelo de mínimos cuadrados ordinarios o el modelo generalizado de mínimos cuadrados ordinarios, asumimos una serie de consideraciones. Una de estas asunciones es la tan conocida «asunción de normalidad».

A pesar de que la gran mayoría de personas relacionadas con el ámbito de la investigación conocen ese término, actualmente existe mucho mal entendimiento acerca de a que se refiere dicha asunción, como evaluarla y que implicaciones puede tener o no su cumplimiento/incumplimiento.

Entendiendo la asunción de normalidad

La asunción de normalidad implica asumir una distribución normal de los residuos del modelo estadístico que se está implementando, o del estadístico del análisis (ej. distribución de la media muestral). Sin embargo, y esto es algo muy importante, no hace referencia a la distribución de los datos de la muestra, ni tampoco a la distribución poblacional de la variable en cuestión.

Vamos a empezar con el caso de un solo grupo con una sola variable, donde queremos estimar el intervalo de confianza de la media muestral. En esta situación, una práctica habitual es analizar si la distribución de dichos datos se aproxima a la normalidad. El razonamiento que se sigue es que, si los datos se aproximan a la normalidad, entonces es plausible asumir que la distribución muestral de la media también. Aunque este razonamiento tiene cierto sentido, no se cumple a la perfección. Es decir, puede ser que la distribución de los datos de nuestra muestra se aproxime a la normalidad y la de la media muestral no o viceversa. Por ejemplo, puede darse la situación de que tengamos una distribución poblacional ligeramente sesgada a la derecha, que derive en una distribución muestral (n = 200) igual de sesgada. A veces en esta situación, la distribución de la media muestral (con n = 200) se aproxima a la distribución normal, indicando el «cumplimiento» de dicha asunción. Aún así, como comentaré más adelante, que dicha asunción pueda ser plausible tampoco es indicativo de que usar tests paramétricos, o basarnos en la media, sea la mejor opción. En este caso concreto, si la muestra esta sesgada, la media no sería el estimador más apropiado de tendencia central, a expensas de la asunción de normalidad.

Con respecto a los residuos, un ejemplo erróneo del análisis de la asunción de normalidad para un ensayo aleatorizado, sería evaluar la distribución de los datos de la muestra para cada grupo de tratamiento y cada momento de medición por separado. Mientras que, el procedimiento adecuado, sería evaluar la normalidad de los residuos del modelo generalizado de mínimos cuadrados ordinarios implementado para analizar esos datos. Basarse en las distribuciones iniciales de los datos podría llevar al investigador a creer que ese modelo generalizado de mínimos cuadrados ordinarios no es apropiado, usando otros análisis que a lo mejor no son más apropiados y pueden tener otros problemas asociados. El motivo por el que se debe analizar esa distribución de los residuos, es porque los errores estándar calculados para, por ejemplo, una diferencia media ajustada entre dos tratamientos, se calculan con dichos residuos, asumiéndose que siguen una distribución normal en algunos análisis.

Analizando la distribución de los datos

La asunción de normalidad se evaluará siempre de los residuos del modelo estadístico a implementar, ya que no podemos evaluar la distribución del estadístico muestral bajo análisis. Existen distintas maneras de evaluar dicha asunción, que ordenadas de mayor utilidad/adecuación a menor serían:

  • Conocer la «naturaleza» de la variable en cuestión.
  • Histogramas y gráficos de densidad con outliers.
  • Gráficos QQ y PP.
  • Medidas de curtosis y asimetría.
  • Shapiro-Wilk y Kolmogorov-Smirnov con la corrección de Lilliefors (NO RECOMENDADOS).

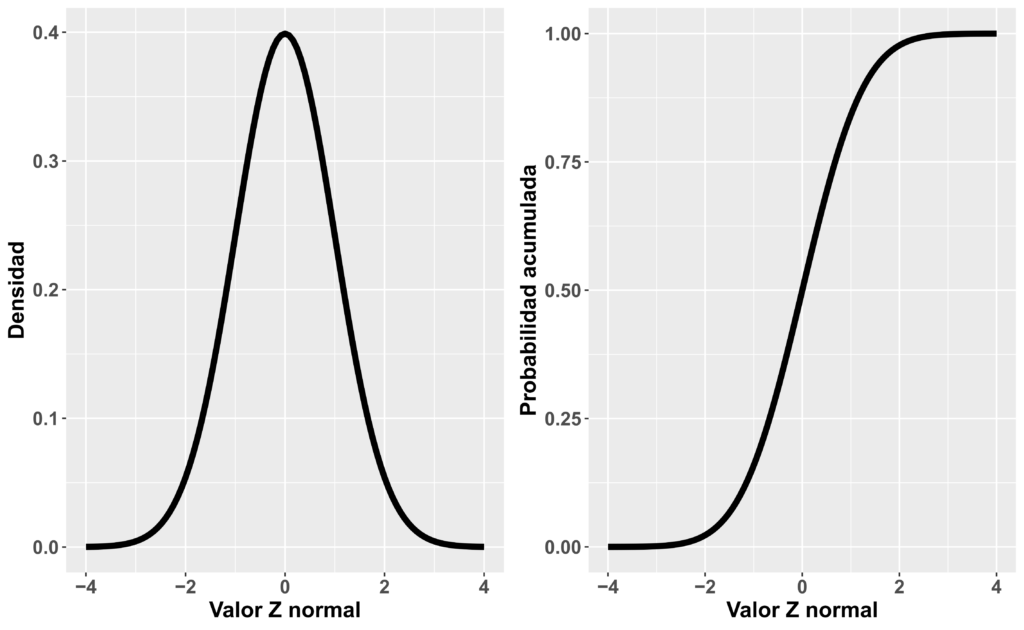
En general, solamente con los puntos segundo y tercero, que consisten en la observación visual de cuatro gráficos, se obtiene la información necesaria y de mayor utilidad para discernir si parece cumplirse o no la asunción de normalidad y en que sentido es distinta la distribución de los residuos (si es más plana, si es asimétrica a la derecha, etc). En otra entrada previa recojo una explicación detallada de los gráficos QQ y PP, que podéis leer haciendo click en el enlace de más arriba, donde también explico brevemente porque los tests de contraste no están recomendados para evaluar la asunción de normalidad.

Las medidas de curtosis y asimetría pueden ser de utilidad, siempre que no se utilicen con una interpretación dicotómica con puntos de corte, ya que ello podría llevar a una malinterpretación y toma de decisiones errónea en la práctica de investigación. No es el objetivo de esta entrada explicar la matemática de los mismos, que me guardo para otra ocasión, de modo que simplemente daré una explicación sencilla de su interpretación.

El coeficiente de curtosis de Fisher nos indicaría como de «achatada» está la distribución de los residuos. El valor de curtosis de la distribución normal es de 3, por ello, normalmente al valor del coeficiente se le resta 3 para centrarlo al cero de cara a su interpretación (*Nota: algunas funciones de R y otros paquetes estadísticos te devuelven el valor original del coeficiente de curtosis, sin restarle 3, esto debe tenerse en cuenta a la hora de interpretar el mismo). Este coeficiente puede tomar los siguientes valores:

  • Curtosis < 0: Distribución más «plana» que la normal, también llamada platicúrtica.
  • Curtosis = 0: Curtosis de la distribución normal, también llamada mesocúrtica.
  • Curtosis > 0: Distribución más «puntiaguda» que la normal, también llamada leptocúrtica.

Por su parte, el coeficiente de asimetría de Fisher-Pearson nos informa del grado de asimetría y la dirección de la misma en la distribución de los residuos. Algunos paquetes estadísticos utilizan una formula que aplica una corrección en función del tamaño muestral. Los valores que puede tomar el estadístico son:

  • Asimetría < 0: Distribución asimétrica hacia la izquierda.
  • Asimetría = 0: Distribución simétrica, como la distribución normal.
  • Asimetría > 0: Distribución asimétrica hacia la derecha.

De cara a su interpretación, no daré ningún punto de corte ya que como he comentado, traen más problemas que soluciones. Cuanto más se alejen los valores de los de la distribución normal, peor. Sin embargo, no hay una regla definida de «cuanto» han de alejarse uno u otro para decidir usar métodos estadísticos que no asuman una distribución normal de los residuos.

Por último y quizás el punto más importante, es el conocimiento técnico de la variable resultado en cuestión. A expensas de los análisis de normalidad, hay variables con ciertas características que deben tenerse en cuenta, ya que implican que las mismas no deban analizarse con métodos que asumen una distribución normal de los residuos (o del estadístico muestral).

Un ejemplo son los cuestionarios auto-reportados por el paciente, tales como el SPADI, el TSK-11, el PCS, etc. Todas estas variables están acotadas tanto superior (máximo valor 100%), como inferiormente (mínimo valor 0%). Este acotamiento implica directamente que la asunción de normalidad no se cumple, aparte de traer consigo el incumplimiento de otras asunciones de los modelos de mínimos cuadrados ordinarios, como son directamente que la variable resultado no esté acotada, el incumplimiento de la asunción de homocedasticidad, y el incumplimiento de la asunción de linealidad (en el caso de varios modelos lineales). Por tanto, toda variable resultado que sea un cuestionario auto-reportado, sería erróneo analizarlo con una regresión lineal múltiple, siendo adecuada la opción de una regresión beta. Además, tampoco sería del todo apropiado en un ensayo clínico aleatorizado analizar las diferencias en dichas variables con un ANOVA, ANCOVA u otros modelos basados en mínimos cuadrados ordinarios. Sin embargo, estos análisis erróneos son los que se ven en casi todas las investigaciones realizadas con estas variables resultado. A día de hoy, desconocemos las implicaciones que puede estar teniendo analizar mal los datos en casi todas las investigaciones de este campo, pudiendo ser que muchas relaciones encontradas no sean tales, y que otras no encontradas si que existan.

Otro ejemplo serían las variables ordinales. Los métodos de análisis estadístico para variables ordinales suelen ser más «complejos» o mejor dicho, no dan la falsa sensación de ser «fácilmente interpretables». Esto hace que muchos investigadores tiendan a utilizar métodos que asumen que la variable en cuestión es una cuantitativa continua, como un ANOVA, ANCOVA o una regresión lineal múltiple, para analizar una variable resultado ordinal, bajo la premisa de que si presenta muchas categorías puede aproximarse a la distribución normal, o bajo ninguna premisa, simplemente porque sí. Aquí quiero hacer un apunte importante, en mayúsculas y directo: ESTO ES MENTIRA. Toda variable ordinal ha de ser tratada como ordinal siempre, con los métodos de análisis estadístico apropiados, tanto en ensayos clínicos como en estudios observacionales. Utilizar métodos de mínimos cuadrados ordinarios en estos casos puede llevar a grandes errores en la obtención de los resultados y las conclusiones extraídas de una investigación. Mi recomendación es que, cualquier análisis realizado de esta manera errónea, no sea en absoluto tenido en consideración. Algunos ejemplos de análisis adecuados para variables ordinales son el «proportional odds model» o el «continuation ratio model».

Aprendiendo con ejemplos de investigación reales

Para ejemplificar estas diferencias entre las distribuciones de los datos muestrales y las de los residuos de los modelos implementados, voy a utilizar tres ejemplos simulados: uno de un análisis pre-post para un solo grupo,  otro de un análisis estilo ANCOVA, con una medición basal y una post-tratamiento con dos grupos a comparar, y un tercero de una regresión lineal múltiple.

Ejemplo 1: Diferencia intra-grupo

Para este ejemplo he simulado una situación en la que tenemos una distribución poblacional de la medición basal y la post-tratamiento que no es normal, con una asimetría izquierda notoria. El objetivo de este estudio es analizar el cambio de la situación basal a la post-tratamiento para un solo grupo. Los análisis de la normalidad de los datos muestrales serían los siguientes:

  • Medición basal:
    • Shapiro-Wilk: p = 0.00143
    • Asimetría: -1.10
    • Curtosis: 0.35
  • Medición post-tratamiento:
    • Shapiro-Wilk: p = 0.01347
    • Asimetría: -0.84
    • Curtosis: -0.19

Los gráficos Q-Q para la medición basal y la post-tratamiento serían los siguientes:

Basándonos en dichos análisis de la distribución de los datos, un investigador podría decidir que no parece ser plausible la asunción de normalidad y decantarse por usar tests no paramétricos (no recomendados) u otras opciones de análisis robustos (recomendadas) sin necesidad.

Veamos ahora que pasa si nos centramos en los residuos del modelo estadístico a implementar, que es en los que se aplicaría en mayor medida la asunción de normalidad. En el caso de un solo grupo y dos mediciones, dichos residuos son la dispersión de la variable diferencia (post – basal). Para evaluar su distribución podemos calcular dicha diferencia para cada individuo y en esa nueva variable aplicar los distintos métodos de análisis de la asunción de normalidad. En este caso tendríamos los siguientes datos:

  • Variable diferencia:
    • Shapiro-Wilk: p = 0.9527
    • Asimetría: -0.08
    • Curtosis: 0.0006

El gráfico QQ para dicha variable diferencia sería el siguiente:

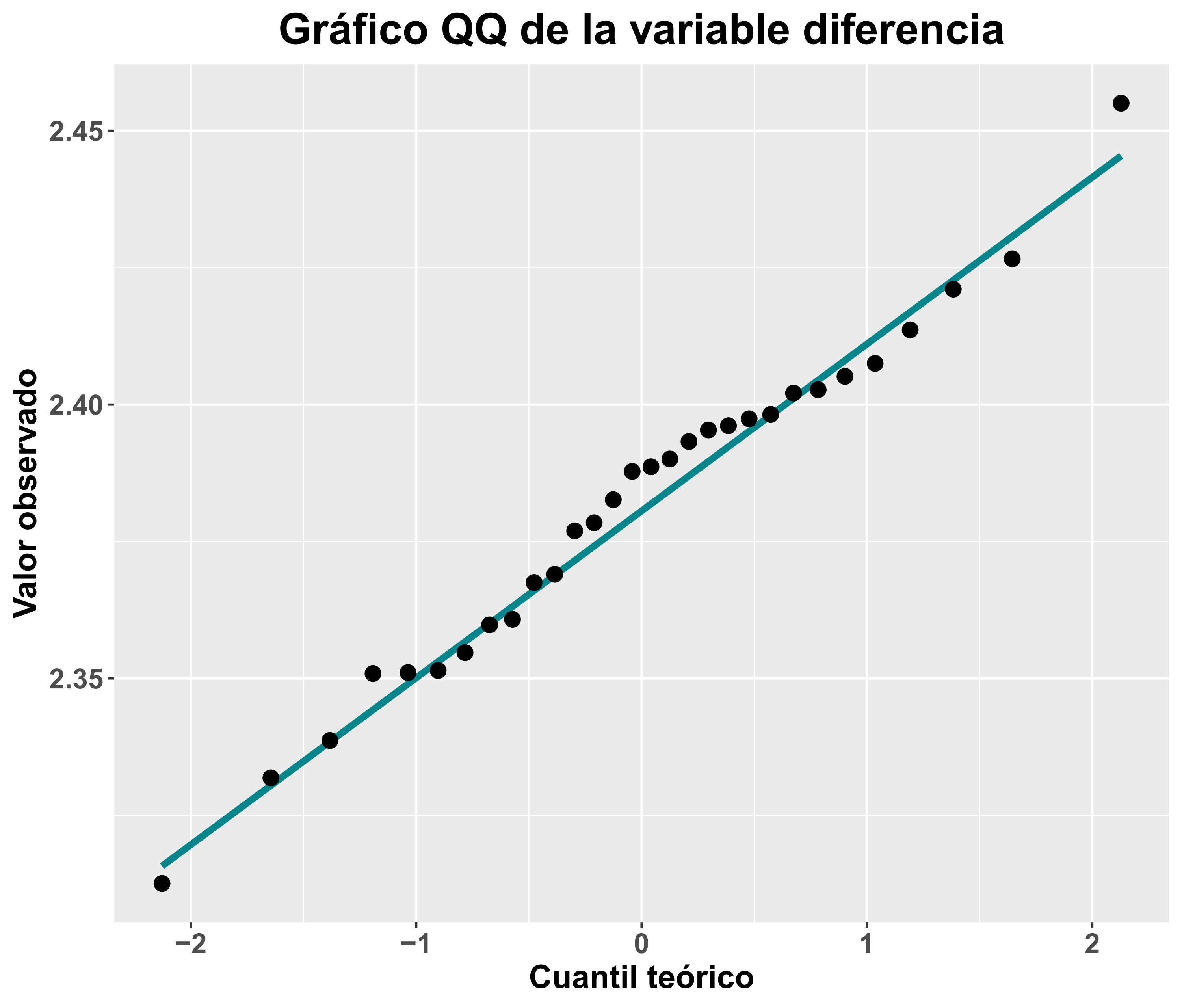
En este caso, las conclusiones que podríamos sacar son muy distintas a las de los análisis iniciales, pareciendo bastante plausible el cumplimiento de la asunción de la normalidad y pudiendo analizarse los datos con una prueba basada en mínimos cuadrados ordinarios.

Ejemplo 2: Modelo estilo ANCOVA

El segundo ejemplo es algo más aproximado a lo que puede ser la situación de un ensayo clínico aleatorizado real. En este ejemplo he simulado datos, también con una distribución poblacional sesgada a la izquierda, para dos grupos en dos momentos, uno antes del tratamiento (medición basal) y otro tras el tratamiento (medición post-tratamiento). Por tanto, tenemos un total de cuatro mediciones. Siguiendo el procedimiento erróneo de evaluar la normalidad de los datos muestrales, se obtienen los siguientes estadísticos:

  • Medición basal grupo 1:
    • Shapiro-Wilk: p = 0.00143
    • Asimetría: -1.10
    • Curtosis: 0.35
  • Medición basal grupo 2:
    • Shapiro-Wilk: p < 0.001
    • Asimetría: -2.07
    • Curtosis: 5.14
  • Medición post-tratamiento grupo 1:
    • Shapiro-Wilk: p = 0.00724
    • Asimetría: -0.86
    • Curtosis: -0.18
  • Medición post-tratamiento grupo 2:
    • Shapiro-Wilk: p < 0.001
    • Asimetría: -2.01
    • Curtosis: 4.97

El modelo de mínimos cuadrados ordinarios que se utilizaría para analizar este estudio sería una regresión lineal de la siguiente manera:

Post-tratamiento = Constante + b1*Basal + b2*Grupo + e

Donde «e» son los residuos del modelo. Implementando dicho análisis de regresión, para obtener diferencias entre-grupos «ajustadas» para la medición basal, podemos extraer los residuos del mismo y llevar a cabo los análisis de la asunción de normalidad en estos. Los resultados serían:

  • Residuos del modelo de mínimos cuadrados ordinarios:
    • Shapiro-Wilk: p = 0.4745
    • Asimetría: 0.25
    • Curtosis: -0.23

Nuevamente, el análisis de los residuos nos orienta a tomar una decisión muy diferente a los análisis de normalidad realizados de la manera equivocada sobre la distribución de los datos muestrales.

Ejemplo 3: Regresión lineal múltiple

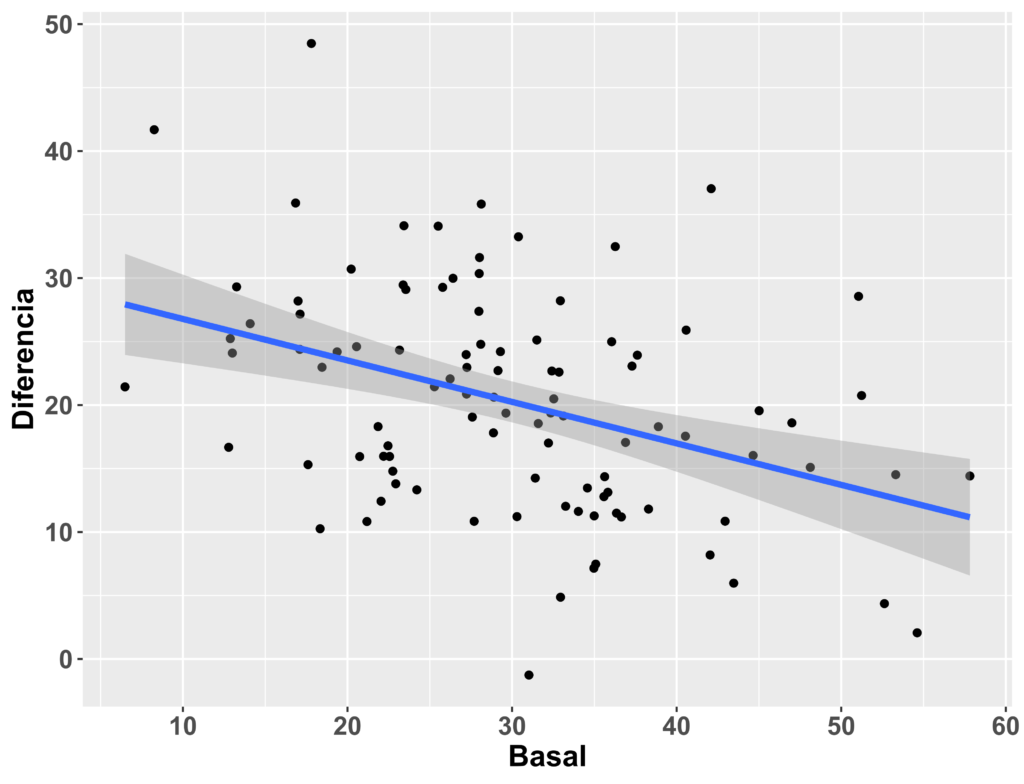
Otra práctica habitual en investigación es analizar la distribución de todas las variables cuantitativas que se han medido, a la hora de realizar un análisis de regresión lineal múltiple. Este procedimiento también sería erróneo. La asunción de normalidad, como se ha comentado, hace referencia a los residuos de dicho modelo de regresión. Estos residuos serían la «parte» que no podemos predecir de cada individuo de la muestra en la variable resultado de interés (ej. fuerza) en función de los predictores incluidos en el modelo (ej. edad, estatura, peso y sexo). Por tanto, todo lo que tiene que ver con la asunción de normalidad en estos modelos, se relaciona únicamente con la variable resultado (fuerza), pero no es necesario para realizar un modelo de mínimos cuadrados ordinarios que las variables predictoras tengan una distribución normal. De ser así, no sería posible incluir ningún predictor categórico, pues estos nunca van a seguir una distribución normal.

La importancia (o no) de la normalidad y la toma de decisiones

Aunque la asunción de la normalidad es una de de las más conocidas por investigadores, no es la «más importante». Muchos métodos basados en mínimos cuadrados ordinarios «funcionan» más o menos bien ante pequeñas desviaciones de dicha asunción, siempre que se cumplan otras asunciones más importantes como la de homocedasticidad. Curiosamente, el resto de asunciones de los modelos de mínimos cuadrados ordinarios no suelen ser tan conocidas, habiendo pocos estudios que analicen adecuadamente la homocedasticidad de los residuos con sus adecuadas estratificaciones pertinentes, o evalúen si quiera otras asunciones como la de linealidad o aditividad (según el modelo implementado). Por eso, aunque a veces existan pequeñas desviaciones, en función de como sean estas y otros aspectos, podemos seguir implementando esos modelos.

Por otro lado, aunque los «análisis de normalidad» salgan favorables para dicha asunción, es erróneo también tomar decisiones solo basándonos en ello. Podemos tener una situación en la que la distribución de los datos (SI, habéis leído bien, LOS DATOS) esté sesgada a la derecha. En este caso, aunque se parezca cumplir la asunción de normalidad de los residuos, puede que debamos considerar que predecir la media (que es lo que predecimos con un modelo de mínimos cuadrados ordinarios) no sea lo más apropiado, ya que no sería un buen estimador de tendencia central, pudiendo ser más oportuno, por ejemplo, utilizar otros modelos de regresión que se basan en la predicción de la mediana.

Dicho de otra manera, la toma de decisiones en investigación de cara a la realización de análisis estadísticos es compleja y no podemos simplificarla, ni a puntos de corte arbitrarios ni a una interpretación aislada de uno, dos o varios análisis. Hay que tener en cuenta el conjunto de información disponible, tanto técnica como a nivel estadístico, para decidir cual es la mejor opción para una situación concreta de investigación.

Conclusión

La asunción de normalidad no hace referencia a la distribución de los datos de la muestra, se refiere a la distribución de lo residuos del modelo estadístico implementado o de la distribución muestral del estadístico bajo análisis. Existen diversas formas de evaluar dicha asunción, siendo algunas más apropiadas que otras. No obstante, debemos siempre tener en cuenta que hay que tener en cuenta otros aspectos para decidir como analizar los datos, ya que la asunción de normalidad no es lo más relevante en esa toma de decisiones en investigación.

Asunción de normalidad

•
marzo 4, 2024
•
Modelo Lineal General, Temas Básicos
•
No hay comentarios

Asunciones: Normalidad En esta entrada se recoge una breve explicación de la tan aclamada asunción de normalidad, haciendo hincapié en a que …

Gráficos QQ y PP

•
diciembre 29, 2023
•
Temas Básicos
•
No hay comentarios

Análisis de la "normalidad": Gráficos QQ y PP En esta entrada se recoge una explicación de los gráficos QQ y PP, útiles …

Minima Diferencia Clinicamente Relevante

•
diciembre 9, 2023
•
Temas Básicos
•
No hay comentarios

Interpretación de la relevancia clínica: El mal uso de la mínima diferencia clínicamente relevante (I) En esta entrada se proporciona una breve …

Calculadora Muestral – Ensayo Aleatorizado

•
agosto 8, 2023
•
Calculadora Tamaño Muestral
•
No hay comentarios

Calculadora Muestral: Ensayos Aleatorizados (diferencia ajustada ancova – precisión) En esta entrada se recoge una breve guía práctica de recomendaciones para calcular …

Categorías
Temas Básicos

Gráficos QQ y PP

Análisis de la "normalidad": Gráficos QQ y PP

En esta entrada se recoge una explicación de los gráficos QQ y PP, útiles para le evaluación de la distribución de los datos y su aparente aproximación a una distribución normal teórica. El análisis de estos gráficos es más adecuado que los tests de contraste de hipótesis de Shapiro-Wilk y Kolmogorov-Smirnov.

Antes de llevar a cabo los análisis estadísticos de una investigación, es necesario evaluar algunos aspectos de los datos, para discernir cual es la mejor manera de analizar los mismos sin inducir sesgos en los parámetros a estimar (ej. medida de tendencia central), y «asegurar en mayor medida» que los errores estándar, intervalos de confianza y valores-p calculados pueden ser adecuados.

Una de estas asunciones, aunque no es la de mayor importancia, es la asunción de la distribución normal de los residuos o de los parámetros a estimar (ej. distribución de la media muestral). Lo más habitual es ver como esta asunción se evalúa con tests de contraste de hipótesis (Shapiro-Wilk o Kolmogorov-Smirnov), aunque este procedimiento no es correcto. Estos tests presentan los siguientes problemas:

  1. Plantean una toma de decisiones dicotómica, sin permitir evaluar el continuo de «cuanto nos alejamos o no del supuesto cumplimiento de la asunción de normalidad».
  2. Se basan en valores-p, cuya mal-interpretación puede llevar a errores en la toma de decisiones con respecto al cumplimiento o no de esta asunción.
  3. No cuantifican la magnitud de la desviación de la asunción de normalidad. Por ejemplo, si tenemos mucha muestra, una pequeña desviación de la asunción de normalidad puede resultar estadísticamente significativa (p < .05), sin que esta tenga que ser relevante, pudiendo ser ignorada por completo tal pequeña desviación. Del mismo modo, una desviación más notoria en una muestra pequeña puede resultar no significativa, pero si tener implicaciones importante de cara a como analizar los datos de esa muestra en concreto.
  4. No informan directamente del incumplimiento de la asunción. Los tests de contraste de hipótesis por si solos no nos dicen nada sobre la verdad/falsedad de las hipótesis en si mismas.

Otra actuación incorrecta pasa por establecer que, si la muestra supera n > 30 sujetos, entonces por el «Teorema Central Límite», podemos asumir que se cumple el supuesto de normalidad. Esta es una afirmación engañosa ya que:

  1. El «Teorema Central Límite» no hace referencia a tal afirmación.
  2. Muestras incluso superiores a 30 sujetos (ej. 50 o incluso 100 sujetos) pueden no derivar en el cumplimiento de dicha asunción si, por ejemplo, la distribución poblacional está muy sesgada a la derecha o la izquierda.
  3. Asumir este punto de corte arbitrario puede llevar a no valuar la distribución de los datos de la muestra, ignorándose incluso otras asunciones más importantes (como la homocedasticidad), que pueden derivar en una estimación sesgada de los parámetros bajo estudio (ej. tendencia central) e inutilidad de los intervalos de confianza calculados.
Gráficos QQ y PP: Definiciones

Una manera más adecuada de analizar la distribución de los residuos de un modelo, para evaluar si parece cumplirse o no el supuesto de distribución normal de los mismos, son los gráficos QQ y PP. Antes de proseguir, cabe destacar que estos gráficos no son lo único que deberíamos evaluar (los histogramas y gráficos de dispersión aportan información muy útil también), y que hay otros aspectos a tener en cuenta como la homocedasticidad, linealidad, aditividad, y presencia de valores atípicos o influyentes, que deberían ser tenidos en cuenta en los modelos que asumen distribución normal de los residuos. Ambos gráficos se basan en comparar unos valores observados, con sus respectivos teóricos bajo una distribución normal.

Los gráficos QQ se construyen enfrentando los cuantiles observados en nuestra muestra, con los cuantiles teóricos esperados bajo una distribución normal. Por otro lado, los gráficos PP se construyen enfrentando las probabilidades acumuladas observadas, con las esperadas bajo una distribución normal. A continuación se muestran dos gráficos, uno que es el gráfico de densidad de la distribución normal (izquierda) y otro a la derecha que es el gráfico de la distribución de la probabilidad acumulada normal. La probabilidad acumulada reflejada a la derecha es el área bajo la curva que queda a la izquierda de cada valor Z de la distribución normal de la gráfica de la izquierda.

Ahora imaginemos que hemos realizado una investigación con unos datos observados (n = 1000), para los cuales calcularemos los mismos gráficos de densidad y probabilidad acumulada. En la siguiente imagen se muestran ambas distribuciones, la normal teórica (rojo) y la observada en la muestra (azul).

Como se puede apreciar, las gráficas no son idénticas (el estudio simulado provenía de una distribución poblacional sesgada hacia la derecha). Centrándonos en la gráfica de la derecha, lo que se muestra en un gráfico PP serían esas diferencias entre ambas gráficas (emparejadas según el valor Z), de forma que si la muestra se aproxima de manera perfecta a una distribución normal, obtendríamos una correlación perfecta entre las probabilidades acumuladas, con todos los puntos del gráfico PP coincidiendo con una línea oblicua que pasa por el punto (0,0) y tiene una pendiente de 1. En la siguiente figura se muestra el gráfico PP para este estudio simulado.

Como se aprecia en este gráfico PP, al inicio la probabilidad acumulada observada es menor que la esperada bajo una distribución normal (puntos por encima de la linea oblicua de relación perfecta), que es lo mismo que podemos observar en las gráficas superpuestas con colores de más arriba.

Ambos gráficos informan sobre lo mismo, las desviaciones de la distribución de los datos con respecto a una distribución normal teórica. El motivo de que haya dos gráficos, es que cada uno pone el foco en una región distinta de la distribución. Los gráficos QQ son más sensibles (permiten visualizar mejor) desviaciones de la normalidad en los extremos de la distribución, mientras que los gráficos PP permiten visualizar mejor desviaciones en el centro de la distribución. En otras palabras, es como si el gráfico QQ hiciera «zoom» en los extremos, y el gráfico PP hiciera «zoom» en el centro.

Esta diferencia se entiende mejor si nos centramos en los gráficos PP. Como se ha comentado, estos enfrentan la probabilidad acumulada. Si asumimos que hay una desviación de la normal, puede haber una diferencia entre la probabilidad acumulada del primer dato ordenado observado (el más pequeño de todos) y la probabilidad esperada bajo la distribución normal. Para el segundo dato, tenemos dos errores, el cometido para el primero y el cometido para la diferencia del primero al segundo (ya que es una probabilidad acumulada y por tanto se van sumando). Resulta por tanto obvio que, si tenemos una desviación de la distribución normal, en el extremo inferior no se apreciarán muchas diferencias en el gráfico PP, porque los errores cometidos son menores que según vamos avanzando hacia el centro de la distribución, donde se van acumulando más posibles errores de desviación de la normal. Siguiendo el mismo razonamiento, como la probabilidad máxima es de 1, según nos acercamos a los valores superiores los errores también serán más pequeños, ya que ambas gráficas tenderán a aproximarse a la probabilidad de 1. Por tanto, donde más apreciaremos diferencias en un gráfico PP es en la zona central de los datos. A continuación se muestran los gráficos QQ y PP para el estudio simulado anteriormente, con una población sesgada hacia la derecha.

Como puede apreciarse, en el gráfico QQ (izquierda) las diferencias entre las distribuciones son más notorias en los extremos, mientras que en el gráfico PP (derecha) la diferencias son más notorias en la región central, tal y como se ha comentado, como si hiciéramos «zoom» en la gráfica en secciones distintas.

En el gráfico QQ la pendiente de la recta es igual a la desviación estándar de la muestra y la ordenada en el origen es igual a la media. Esto es así porque, en lugar de enfrentar directamente los cuantiles, se suele mantener las unidades originales en los datos observados en el eje Y.

El tamaño muestral y la variabilidad de los gráficos QQ y PP normales

Incluso cuando se cumple el supuesto de normalidad, la distribución de los datos puede alejarse de la supuesta distribución normal, por errores debidos al muestreo aleatorio. Según se vaya incrementando el tamaño muestral, si la asunción de normalidad se cumple, los gráficos QQ y PP deberían aproximarse más a la línea oblicua de concordancia perfecta entre las distribuciones.

A continuación se muestran los gráficos QQ y PP para 100 estudios simulados (bajo el cumplimiento de la asunción de normalidad) con tamaños muestrales de 10, 30 y 100 sujetos.

Como se puede apreciar, a mayor tamaño muestral mas aproximación hay entre las distribuciones observadas en la muestra y la teórica normal. Un punto a destacar es los extremos de los gráficos QQ, que somo se observa, incluso para un tamaño muestral de n = 100, se aprecian desviaciones de la línea recta de concordancia perfecta entre las distribuciones. Esto se debe a que por lo general, debido al muestreo, se tienden a obtener valores más extremos en las colas que los esperados bajo una distribución normal teórica, es decir, que los cuantiles observados son más grandes (positivo o negativo) que los teóricos, en los extremos de la distribución. Por ello, debemos tener en cuenta que un patrón como el mostrado en estas figuras en los gráficos QQ, con algunos puntos por debajo de la recta en el extremo inferior y por encima de la misma en el extremo superior de la distribución, es algo «normal».

Gráficos QQ y PP para algunos tipos de distribuciones

A modo de facilitar la comprensión de como pueden influir algunas desviaciones de la distribución normal en los gráficos QQ y PP, se muestran a continuación ambos gráficos para simulaciones de n = 1000 de: muestra sesgada a la derecha, muestra sesgada a la izquierda, muestra platicúrtica y muestra leptocúrtica. Cabe destacar que estas gráficas son con un tamaño muestral elevado, si se llevasen a cabo muestreos aleatorios con un tamaño menor (ej. n = 10 o n = 30) de poblaciones con estas distribuciones, lo que podríamos observar en los gráficos QQ y PP podría variar notoriamente. 

Recomendaciones de buenas prácticas

A continuación nombraré algunas recomendaciones de buenas prácticas de cara a investigadores en relación a la temática de la entrada.

  1. Análisis descriptivo detallado de todas las variables de estudio. En cualquier investigación es totalmente indispensable realizar y tener en cuenta un análisis descriptivo exhaustivo de todas las variables medidas. Este análisis debe incluir como mínimo (por separado para cada grupo, y también para los residuos de los modelos multivariables implementados):
    1. Media, mediana, desviación estándar, primer y tercer cuartiles, rango, y medidas de curtosis y asimetría.
    2. Gráficos QQ (obligatorio) y PP (opcional).
    3. Histogramas y/o gráficos de dispersión.
    4. Análisis de valores atípico
  2. No usar Shapiro-Wilk ni Kolmogorov-Smirnov para evaluar la asunción de normalidad.
  3. No basarnos en el «Teorema Central Límite» para asumir el cumplimiento de la asunción de normalidad.
  4. No usar de manera aislada los gráficos QQ y PP. Estos gráficos aportan una información, pero no toda. Para decidir si asumimos el cumplimiento o no de la asunción de normalidad hay que evaluar el conjunto de características de la distribución de la muestra.
  5. Primar siempre el conocimiento técnico para decidir sobre la distribución teórica asumida. A expensas de los análisis de la distribución de los datos, debe primar siempre nuestro conocimiento técnico sobre la variable resultado de interés. Por ejemplo, los cuestionarios auto-reportados por el paciente son variables acotadas superior e inferiormente, algo que induce heterocedasticidad y una distribución no normal (es más plausible una distribución beta), de modo que analizarlas como dependientes con modelos de regresión de mínimos cuadrados ordinarios es inapropiado, a expensas de los análisis descriptivos de los residuos.
  6. Son preferibles los gráficos QQ a los PP. Por lo general, lo que más «problemas» puede dar y que más interesa mirar son los extremos de la distribución. Por ello, suele ser preferible reportar y analizar los gráficos QQ a los PP. Lo adecuado sería analizar ambos, y lo inadecuado analizar y reportar solo los PP, ya que pueden sesgar al investigador y al lector.
  7. Evaluar el resto de asunciones del modelo implementado. Como se ha comentado, la asunción de la distribución normal de los residuos es solo una de las múltiples que se hacen al implementar algunos modelos de análisis estadístico. El resto de asunciones deben ser evaluadas adecuadamente, ya que por lo general esas otras asunciones (como la homocedasticidad, linealidad o aditividad) suelen ser más importantes que la de la distribución normal.
Conclusiones

La evaluación de la asunción de la distribución normal de los residuos no debe realizarse con test de contraste de hipótesis como Shapiro-Wilk o Kolmogorov-Smirnov, ni basarse en puntos de corte arbitrarios como el supuesto «Teorema Central Límite». Es importante conocer y analizar los gráficos QQ y PP para poder discernir si parecen haber desviaciones de la asunción de normalidad que merezcan ser tenidas en consideración de cara a la realización de los análisis estadísticos.

Asunción de normalidad

•
marzo 4, 2024
•
Modelo Lineal General, Temas Básicos
•
No hay comentarios

Asunciones: Normalidad En esta entrada se recoge una breve explicación de la tan aclamada asunción de normalidad, haciendo hincapié en a que …

Gráficos QQ y PP

•
diciembre 29, 2023
•
Temas Básicos
•
No hay comentarios

Análisis de la "normalidad": Gráficos QQ y PP En esta entrada se recoge una explicación de los gráficos QQ y PP, útiles …

Minima Diferencia Clinicamente Relevante

•
diciembre 9, 2023
•
Temas Básicos
•
No hay comentarios

Interpretación de la relevancia clínica: El mal uso de la mínima diferencia clínicamente relevante (I) En esta entrada se proporciona una breve …

Calculadora Muestral – Ensayo Aleatorizado

•
agosto 8, 2023
•
Calculadora Tamaño Muestral
•
No hay comentarios

Calculadora Muestral: Ensayos Aleatorizados (diferencia ajustada ancova – precisión) En esta entrada se recoge una breve guía práctica de recomendaciones para calcular …

Categorías
Temas Básicos

Minima Diferencia Clinicamente Relevante

Interpretación de la relevancia clínica: El mal uso de la mínima diferencia clínicamente relevante (I)

En esta entrada se proporciona una breve explicación de la limitada, incluso ausencia, de utilidad de los valores conocidos como Mínima Diferencia Clínicamente Relevante (o Importante) para discernir si un paciente mejora en la práctica clínica o interpretar los resultados de una investigación.

Uno de los retos a los que se enfrentan tanto clínicos como investigadores es dar respuesta a siguiente pregunta: ¿Son mis hallazgos relevantes? Tanto si se está tratando a un paciente y se observa una mejoría en una variable (ej. intensidad del dolor, grado de discapacidad…), como si se está realizando un ensayo clínico aleatorizado y se encuentra una mejoría estadísticamente significativa de un tratamiento con respecto a otro, debemos decidir si esas diferencias son o no relevantes y merecen ser tenidas en consideración. Por ejemplo, puede ser que existan diferencias medias entre dos tratamientos para un problema musculoesquelético concreto, pero que sean tan pequeñas (ej., 0.3 cm en una EVA), que no sirvan para guiarnos en la práctica clínica con respecto a que intervención es mejor aplicar, y por tanto no podamos concluir que una intervención parece ser mejor que la otra.

Una de las propuestas que se han hecho desde hace décadas para dar respuesta a esta pregunta es la Mínima Diferencia Clínicamente Relevante (MDCR). De manera simplificada, este concepto viene a definir un punto de corte en una variable concreta, por encima del cual se considera que la mejoría de un paciente o diferencia de medias entre dos tratamientos es relevante y debe ser tenida en consideración en nuestra práctica clínica. Existen varias propuestas estadísticas para realizar su cálculo, que no son el objetivo de esta entrada, motivo por el cual no serán abordadas.

De estos métodos propuestos, el más utilizado dentro del campo de ciencias de la salud es el denominado método de anclaje (anchor-based). Este método, de manera simplificada, consiste en relacionar la mejoría observada de cada sujeto de un estudio de investigación, con otra variable que se considera «gold standard», el cual asumimos que nos informa de manera más directa de la relevancia clínica del hallazgo en cuestión en dicha variable resultado. Dentro de estos «gold standard», el más utilizado en ciencias de la salud es la Percepción de Mejoría del Paciente, que puede medirse con distintas herramientas basadas en preguntar al paciente cuanto percibe que ha mejorado/empeorado y que, finalmente, acaban dividiendo a los sujetos en dos grupos: aquellos que refieren una percepción de mejoría y aquellos que no. En función de esta clasificación en dos grupos, se calcula un punto de corte que «optimiza» la predicción de la mejoría por parte del paciente en función de la variable resultado que nos interesa (ej. EVA para intensidad del dolor). Ese punto de corte es lo que se conoce como MDCR.

Sin embargo, existe un problema, ya que nunca se consigue una predicción perfecta de esa percepción de mejoría por parte del paciente. Es decir, habrá personas que tengan una mejoría por debajo de dicho punto de corte y, sin embargo, refieran encontrarse mucho mejor y al revés, personas que reporten una mejoría por encima de dicho punto de corte pero que no perciban encontrarse mejor. Esta ausencia de relación perfecta entre ambas variables, de capacidad de discriminación perfecta de los sujetos que perciben encontrarse mejor y aquellos que no, es lo que hace que la MDCR calculada según los pasos mencionados carezca de utilidad alguna, tanto en la práctica clínica como en investigación.

Sin embargo, no debemos preocuparnos porque dicho valor, la MDCR, sea totalmente inútil para su propósito, ya que disponemos de una solución más adecuada, sencilla y rápida, que hemos tenido siempre al alcance de nuestra mano. La pregunta que queríamos responder sería, ¿mis pacientes perciben esta mejoría como relevante? y las opciones de dar respuesta para los clínicos y los investigadores serían:

  • Clínicos: Si queréis conocer la percepción de mejoría del paciente que estáis tratando, solo tenéis que preguntarle.
  • Investigadores: Si queréis evaluar si la mejoría con un tratamiento se percibe como mejor por parte de los pacientes en comparación a la mejoría obtenida con otro tratamiento, podéis medir directamente en vuestras investigaciones la Percepción de Mejoría del Paciente con cualquiera de las escalas ordinales disponibles.

Conclusiones

El concepto de MDCR utilizando métodos de anclaje con un «gold standard« de percepción de mejoría del paciente carece de utilidad, tanto en la práctica clínica como en investigación. No existe necesidad de «predecir» algo que podemos medir de manera directa siempre.

 

Asunción de normalidad

•
marzo 4, 2024
•
Modelo Lineal General, Temas Básicos
•
No hay comentarios

Asunciones: Normalidad En esta entrada se recoge una breve explicación de la tan aclamada asunción de normalidad, haciendo hincapié en a que …

Gráficos QQ y PP

•
diciembre 29, 2023
•
Temas Básicos
•
No hay comentarios

Análisis de la "normalidad": Gráficos QQ y PP En esta entrada se recoge una explicación de los gráficos QQ y PP, útiles …

Minima Diferencia Clinicamente Relevante

•
diciembre 9, 2023
•
Temas Básicos
•
No hay comentarios

Interpretación de la relevancia clínica: El mal uso de la mínima diferencia clínicamente relevante (I) En esta entrada se proporciona una breve …

Calculadora Muestral – Ensayo Aleatorizado

•
agosto 8, 2023
•
Calculadora Tamaño Muestral
•
No hay comentarios

Calculadora Muestral: Ensayos Aleatorizados (diferencia ajustada ancova – precisión) En esta entrada se recoge una breve guía práctica de recomendaciones para calcular …

Categorías
Calculadora Tamaño Muestral

Calculadora Muestral – Ensayo Aleatorizado

Calculadora Muestral: Ensayos Aleatorizados (diferencia ajustada ancova - precisión)

En esta entrada se recoge una breve guía práctica de recomendaciones para calcular el tamaño muestral mínimo necesario para un ensayo clínico aleatorizado, en función de la precisión deseada de una diferencia de medias ajustada para la medición basal.

En esta página se presenta una aplicación Shiny que he creado para calcular el tamaño muestral mínimo necesario para un ensayo clínico aleatorizado (ECA), en función de la precisión deseada de una diferencia de medias ajustada de un Análisis de la Covarianza (ANCOVA). El motivo de que se presente para este tipo de análisis es debido a los siguientes motivos:

  1. Las interacciones tiempo-por-grupo tienen una peor interpretación clínica para guiar los cálculos.
  2. La potencia para detectar una diferencia de medias es menor que para detectar una interacción tiempo-por-grupo.
  3. El ajuste de la medición basal mediante un ANCOVA mejora la precisión en la estimación de la diferencia entre-grupos.

La aplicación se basa en la función ‘ss.aipe.c.ancova’ del paquete de R ‘MBESS’ creado por Ken Kelley, que se basa en la amplitud deseada del intervalo de confianza con una potencia estadística deseada.

Material de Información

Paquete R ‘MBESS’: MBESS: The MBESS R Package version 4.9.2 from CRAN (rdrr.io)

Función ‘ss.aipe.c.ancova’: ss.aipe.c.ancova in MBESS: The MBESS R Package (rdrr.io)

Artículo: Lai & Kelley (2011). Accuracy in parameter estimation for ANCOVA and ANOVA contrasts: Sample size planning via narrow confidence intervals.

Guía resumen para el cálculo

La precisión de una diferencia de medias entre-grupos ajustada para la medición basal, mediante un análisis tipo ACOVA (o lo que es lo mismo, una regresión lineal), se ve incrementada en una magnitud de √1−𝜌2 en un ensayo aleatorizado, siendo 𝜌 la correlación entre la medición basal y la post-tratamiento.(Borm et al., 2007) Es por ello que el cálculo planteado se realiza en base a dicha diferencia de medias ajustadas, en lugar de a una diferencia de medias post-tratamiento sin ajustar.

El primer parámetro a tener en consideración es la desviación estándar de la variable resultado de interés. A menor desviación estándar, mayor precisión, de modo que debemos procurar no infraestimar este parámetro a la hora de realizar los cálculos, para no obtener una muestra más pequeña de lo necesario. La recomendación es revisar la literatura previa publicada con tratamientos, momentos de seguimiento y variables resultado similares para estimar un valor plausible. Los estudios con poca muestra tienden a infraestimar el valor de la desviación estándar. Existen dos propuestas para corregir dicha infraestimación, cuya implementación puede ser recomendable incluso aunque se extraigan los datos de desviación estándar de ensayos aleatorizados y no de estudios piloto.(Whitehead et al., 2015)

El segundo parámetro a especificar es la correlación (𝜌) entre la medición basal y la post-tratamiento. A mayor correlación, mayor precisión y por lo tanto menor muestra necesaria. Debemos procurar no sobre-estimar el valor de la correlación para evitar obtener muestras demasiado pequeñas. Según se incrementa la distancia temporal entre la medición basal y la post-tratamiento, el valor de dicha correlación tiende a disminuir. En el artículo de Walters et al. del año 2019 se ofrece una revisión detallada sobre los valores plausibles de correlación para variables resultado auto-reportadas por el paciente. Una recomendación conservadora y plausible es usar un valor de 𝜌 = 0.50, para seguimientos iguales o inferiores a 2 años, y de 𝜌 = 0.40 para seguimientos superiores a 2 años. No obstante, este valor puede ser contrastado y definido en base a literatura previa publicada con una metodología similar al ensayo clínico a realizar.

El tercer parámetro a especificar es el valor del MoE deseado, que sería la mitad de la amplitud del intervalo de confianza. Este valor es el más complejo de especificar, ya que es difícil saber cual es margen aceptable de precisión, pues esto depende de múltiples factores contextuales, pudiendo variar mucho de una población a otra, o según el tipo de tratamiento implementado. A mayor MoE menor muestra necesaria, ya que disminuimos la precisión que esperamos obtener, de forma que debemos procurar no sobre-estimar el valor de MoE deseado. No se pueden dar recomendaciones de un valor mínimo de MoE adecuado, pero si algunas recomendaciones de como no especificar dicho MoE. La pregunta que debemos hacernos para establecer el MoE sería: ¿Cambiarían las conclusiones que sacaría de mi estudio si el valor de la diferencia de medias observada variase en una magnitud de +/- el valor del MoE? Si la respuesta es no, entonces ese valor de MoE es aceptable. El MoE no debe ser establecido en función de la mínima diferencia detectable, debido a que a mayor error de medición, mayor valor de la mínima diferencia detectable y por tanto menos muestra necesaria, infraestimándose aun más el cálculo. Por otro lado, también debe tenerse cautela al usar directamente la de mínima diferencia clínicamente relevante, ya que también son valores orientados a diferencias individuales y no muestrales.

En relación al MoE, está el concepto de potencia asociada al MoE esperado, que tiene una interpretación al concepto clásico de potencia, salvo que en lugar de para una diferencia media, para una amplitud esperada del intervalo de confianza. Una recomendación conservadora es usar una potencia del 80%. Si se especifica un valor del 50% estaríamos ignorando el concepto de potencia, y el cálculo sería simplemente un cálculo de precisión sin potencia considerada, como el que ofrecen otros paquetes de R o programas como Epidat para algún estadístico.

Otro parámetro a especificar es el X% de confianza del intervalo de confianza, que por defecto está establecido en el 95%. Esta calculadora está basada para la diferencia entre dos grupos, si el ensayo aleatorizado tuviera más de dos grupos, el procedimiento sería seleccionar aquellos dos de mayor relevancia (o que más muestra necesitasen) para realizar el cálculo, y ampliar la muestra necesaria para el tercer grupo. Si se dispone de más de dos grupos y se desea realizar alguna corrección para tasas de error esperadas, la recomendación es utilizar la corrección de Bonferroni a la hora de especificar el X% de confianza del intervalo. Por ejemplo, si disponemos de tres grupos, el X% quedaría definido como 1-0.05/3 = 0.9833, en lugar del valor predefinido de 0.95.

Finalmente, el último parámetro a especificar es el porcentaje de pérdidas esperado, cuyo valor conservador está predefinido en 0.15, siendo plausibles y recomendables valores entre 0.10 y 0.20.

Con todos estos parámetros especificados, la calculadora devolvería el tamaño muestral mínimo necesario por grupo para realizar el ensayo aleatorizado.

¡IMPORTANTE!

Las aplicaciones Shiny funcionan mediante un sistema de suscripción, donde se «alquila» un periodo de tiempo mensual de utilización de las mismas. Por favor, una vez realizado el cálculo, asegúrate de cerrar la pestaña del explorador para no gastar un tiempo innecesario y que más personas puedan utilizar la aplicación si lo necesitan. ¡Muchas gracias!

Calculadora para Ensayos Aleatorizados

Parámetro a especificar Descripción
Desviación estándar (Grupo Experimental)
Desviación estándar post-tratamiento del grupo experimental.
Desviación estándar (Grupo Control)
Desviación estándar post-tratamiento del grupo control.
Correlación
Correlación entre la medición basal y la post-tratamiento.
MoE Esperado
Mitad de la amplitud del intervalo de confianza deseada.
Nivel del intervalo de confianza
Porcentaje del intervalo de confianza deseado. Por defecto = 0.95.
Potencia para el MoE esperado
Potencia deseada para obtener un MoE igual o inferior al esperado. Por defecto = 0.80.
Porcentaje esperado de pérdidas
Porcentaje esperado de pérdidas para corregir el cálculo de tamaño muestral. Por defecto = 0.15.
¡Accede a la Calculadora!

Asunción de normalidad

•
marzo 4, 2024
•
Modelo Lineal General, Temas Básicos
•
No hay comentarios

Asunciones: Normalidad En esta entrada se recoge una breve explicación de la tan aclamada asunción de normalidad, haciendo hincapié en a que …

Gráficos QQ y PP

•
diciembre 29, 2023
•
Temas Básicos
•
No hay comentarios

Análisis de la "normalidad": Gráficos QQ y PP En esta entrada se recoge una explicación de los gráficos QQ y PP, útiles …

Minima Diferencia Clinicamente Relevante

•
diciembre 9, 2023
•
Temas Básicos
•
No hay comentarios

Interpretación de la relevancia clínica: El mal uso de la mínima diferencia clínicamente relevante (I) En esta entrada se proporciona una breve …

Calculadora Muestral – Ensayo Aleatorizado

•
agosto 8, 2023
•
Calculadora Tamaño Muestral
•
No hay comentarios

Calculadora Muestral: Ensayos Aleatorizados (diferencia ajustada ancova – precisión) En esta entrada se recoge una breve guía práctica de recomendaciones para calcular …

Categorías
Avanzado Ensayos Clínicos Inferencias Modelo Lineal General Temas Avanzados Uncategorized

Cambio Intra- & Entre-Grupos en Ensayos Aleatorizados

Ensayos aleatorizados: Cambio intra- & entre-grupos

En esta entrada se recoge una breve explicación de los cambios intra-grupos y entre-grupos dentro del contexto de un ensayo aleatorizado, haciendo hincapié en su finalidad, limitaciones y adecuada interpretación.
De la práctica clínica a los ensayos aleatorizados

En la práctica clínica, la forma que disponemos de saber si un paciente mejora, es tomar una medición basal de referencia y una o varias mediciones en distintos momentos posteriores de seguimiento. Después, podemos observar la diferencia de dichas mediciones posteriores con la situación basal, para ver si ha habido un cambio en dicha variable. Sin embargo, a que se debe dicho cambio, pudiendo ser a un efecto de la intervención aplicada, historia natural, errores en el procedimiento de medición, etc. También puede deberse a una combinación de estos, influyendo algunos más y otros menos, por ejemplo:

Para poder saber cuál es la efectividad de la intervención, si es que hay alguna, debemos poder restar a dicha mejoría observada el efecto atribuible a otros factores, como los errores de medición o la historia natural. Sin embargo, esto no puede realizarse con un solo grupo de sujetos, ya que no tenemos forma de saber cuánto ha influido cada factor, por ello es necesario contar con un grupo no expuesto a la intervención, pero si a los otros factores que pueden influir en que los pacientes cambien a lo largo del tiempo. Esto es lo que se realiza en un ensayo clínico aleatorizado. Por ejemplo, podemos comparar un programa de ejercicio (grupo experimental) con un grupo que no reciba tratamiento (grupo control). La mejoría del grupo de ejercicio podría ser la siguiente:

Como se ha comentado, no sabemos cuándo ha contribuido cada factor a dicha mejoría y si hay o no algún efecto del tratamiento. La mejoría del grupo control podría ser esta: 

Dado que lo único que diferencia (si se ha realizado bien el estudio) al grupo experimental del control, es la aplicación de ejercicio terapéutico, si calculamos la diferencia entre ambos podremos obtener una estimación del efecto de la intervención:

Diferencias intra-grupo dentro del contexto de un ensayo clínico aleatorizado

Como se ha comentado, las diferencias intra-grupo no nos aportan información sobre la efectividad de una intervención, siendo esta información aportada por las diferencias entre-grupos. Entonces, ¿Qué utilidad tienen las diferencias intra-grupo en un ensayo aleatorizado?

Utilidad de la medición basal (antes de la intervención)

En contra de la intuición, las mediciones basales, antes de aplicar el tratamiento, no son en absoluto necesarias para poder evaluar la efectividad de una intervención en un ensayo aleatorizado. Se puede realizar un estudio aleatorizado midiendo solo a los 3 meses de haber aplicado la intervención, y poder obtener estimaciones precisas de la efectividad de esta.

Volviendo a la práctica clínica, si tenemos dos sujetos, uno que con una intensidad de dolor post-tratamiento de 3 y otro de 2.9 podríamos pensar que ambos han mejorado por igual, sin embargo, nos faltaría un dato, la situación de dolor basal de la que partían. Si uno de los sujetos partía de una intensidad de 8 y el otro de 4, las mejorías de uno y otro serían 5 y 2.1, habiendo claras diferencias (aunque no sabríamos si la mejoría sería por el tratamiento). Es decir, el calcular el cambio intra-grupo, con respecto a la medición basal, es una forma de “ajustar” o “controlar” para posibles diferencias en la situación basal, ya que la diferencia de los sujetos en el post-tratamiento depende de sus diferencias en la situación basal, y sin tener en cuenta la misma entonces podríamos malinterpretar quien ha mejorado más o menos.

En un ensayo aleatorizado, ese control de la situación basal se realiza mediante el proceso de asignación aleatoria a los grupos de tratamiento, que hace que la asignación al tratamiento sea independiente de la situación basal de los sujetos en la variable de interés y en todas las variables confusoras (medidas o sin medir en el estudio). Por ello, en este tipo de diseños no sería necesario como se ha comentado una medición basal para poder analizar la efectividad de un determinado tratamiento, pudiéndose analizar simplemente las diferencias post-tratamiento entre los grupos.

El motivo por el cual se realiza una medición basal, antes de aplicar la intervención, es porque de esta forma podemos mejorar la potencia estadística, siendo más fácil encontrar un efecto de la intervención bajo estudio, si es que existe alguno. Es decir, se realiza para disminuir el número de sujetos necesarios para llevar a cabo la investigación.

Cuando se dice que la aleatorización hace que la asignación al tratamiento sea independiente de la situación basal, implica decir que la diferencia media esperada (“real”) entre los grupos en la situación basal es de cero. Se habla de diferencia media esperada porque es el valor al que tiende dicho estadístico cuando el tamaño muestral tiende a infinito, sin embargo, en investigación las muestras nunca suelen ser tan grandes y, por tanto, siempre se observan pequeñas diferencias en la situación basal entre los grupos, originadas por la asignación aleatoria. Como sabemos que la diferencia real es de cero, si medimos la situación basal (previa al tratamiento), podemos incluir esa variable en un tipo de análisis conocido como Análisis de la Covarianza, para forzar a que dicha diferencia será cero en la situación basal en nuestro estudio, ajustándose las diferencias post-tratamiento y la precisión en la estimación de estas, mejorando la potencia estadística de los ensayos clínicos y, por tanto, necesitándose menos muestra. 

Los cambios como un modelo de regresión

Cuando calculamos la diferencia en dos momentos de tiempo de una variable, el objetivo es “ajustar” o “controlar” para la situación basal. En la práctica clínica normalmente medimos a un paciente varias veces, de modo que solo podemos realizar esta resta. Sin embargo, en una investigación se suele medir a un conjunto de pacientes (una muestra), siendo este procedimiento de resta simple inadecuado.

Desde un punto de vista de un modelo de regresión lineal, la medición post-tratamiento (Ypost) puede definirse como:

$$Y_{post} = C + b_1*Y_{basal} + error$$

Cuando calculamos manualmente la diferencia (post- menos basal) de cada sujeto, estamos asumiendo el siguiente modelo:

$$Y_{post} – Y_{basal} = C + error$$

La única forma de que las dos ecuaciones se igualen, es que b1 (el coeficiente de regresión sin estandarizar) sea igual a 1, algo que rara vez sucede en la práctica. Dado que el objetivo de calcular el cambio post- menos basal es “controlar” para discrepancias en la situación basal, eso implica que la variable “Diferencia” obtenida, debe ser independiente de la situación basal (correlación = 0), algo que solo sucederá si b1 = 1. De no ser así, habrá una relación entre la diferencia y la situación basal, como se muestra a continuación con datos simulados:

Esto tiene dos implicaciones. Por un lado, sigue habiendo dependencia con la situación basal, pudiéndose sobreestimar o infraestimar el posible efecto de la intervención, y por otro, no se minimizarían los errores del modelo de regresión, disminuyendo por tanto la precisión y potencia estadística del estudio.

Los ensayos aleatorizados como un modelo de regresión

Partamos ahora del contexto de un ensayo aleatorizado, donde se van a comparar dos grupos,  uno que recibe un tratamiento experimental y un grupo control sin tratamiento, tomándose mediciones en la situación basal y a los 6 meses de seguimiento. En este caso tenemos tres posibilidades para comparar ambos grupos: ver las diferencias en el post-tratamiento, calcular el cambio del post- con respecto a la medición basal y ver las diferencias entre los grupos en esta nueva variable, o utilizar un análisis de la covarianza. El modelo de regresión de cada una de estas opciones sería:

Comparar POST-

$$Y_{post} = C + b_1*Tratamiento$$

Comparar CAMBIO

$$Y_{post} – Y_{basal} = C + b_1*Tratamiento$$

Modelo ANCOVA

$$Y_{post} = C + b_1*Tratamiento + b_2*Y_{basal}$$

En el primer caso (POST-), se asume que la relación entre la medición post-tratamiento y la medición basal es de cero (b2 = 0); en el segundo caso, como se comentaba en el apartado anterior, se asume que b2 es igual a 1; y finalmente en el tercer caso, se deja al modelo de regresión calcular la mejor estimación posible de b2, en lugar de asumir un valor concreto, para minimizar los errores del modelo. En los tres casos, el coeficiente b1 sería la diferencia media entre ambos grupos.

Como se comentaba al inicio de la entrada,  no es necesario tomar mediciones basales para poder evaluar la efectividad de una intervención en un ensayo aleatorizado, siendo también innecesario el cálculo de la diferencia con respecto a la medición basal, teniendo estos procedimientos simplemente la utilidad de mejorar la potencia estadística y precisión (cuando la correlación entre la medición post- y la basal no es igual a cero). En otras palabras,  si la muestra es lo suficientemente grande, dará igual que evaluemos solo las diferencias post-tratamiento, ya que la asignación aleatoria asegura una diferencia basal nula cuando la muestra tiende a infinito. Por ejemplo, asumiendo una diferencia media de 0.5 y una desviación estándar de 1, la muestra necesaria para una potencia deseada del 90%, en función de la correlación entre la medición basal y la post-tratamiento, para cada uno de los tres modelos sería:

Como se puede apreciar en el gráfico, el modelo de ANCOVA optimiza la disminución de los errores del modelo, requiriéndose siempre menos muestra salvo que la correlación sea de 0 o de 1, donde tendría la misma utilidad que el modelo POST-tratamiento o el modelo CAMBIO, pero no menos utilidad. Dado que la potencia estadística solo puede ir de 0 a 100, si incrementásemos mucho el tamaño muestral (ej. 10,000 sujetos por grupo) daría igual que modelo utilizásemos en un ECA, ya que la potencia tendería a su limite superior de 100, siendo las diferencias entre los 3 métodos irrelevantes. Sin embargo, esta no suele ser la situación habitual en la práctica, donde al haber menos muestra, se pueden observar pequeñas diferencias a nivel basal entre los grupos, siendo recomendable por tanto el uso del ANCOVA que minimizaría los errores del modelo con respecto a los otros dos.

Centrándonos ahora en los coeficientes b1 de los tres modelos, es decir, en las diferencias medias entre los grupos, también se observa algo contraintuitivo. Tendemos a pensar que es algo distinto calcular las diferencias entre grupos del cambio con respecto a la medición basal, a calcular las diferencias solo en el post-tratamiento, o mediante el uso del ANCOVA, sin embargo, todos esos procedimientos están estimando lo mismo, el efecto de la intervención, es decir, si incrementamos la muestra lo suficiente, los coeficientes b1 de cada uno de los 3 modelos tenderán todos hacia un mismo valor, estiman lo mismo. Lo único distinto es que cambia la precisión de la estimación y por eso se obtienen pequeñas diferencias de dichos coeficientes en un ensayo clínico realizado, pero a nivel conceptual son lo mismo. Por tanto, la creencia popular de que calcular el cambio con respecto a la situación basal para comparar dicha variable entre dos tratamientos, ofrece una visión más “real” de la efectividad de una intervención, porque estamos comparando mejorías en el tiempo, no se sostiene.

Los engaños de las diferencias intra-grupo en los ensayos aleatorizados

Como se explicaba al inicio del texto, la asignación aleatoria a los grupos de tratamiento es lo que garantiza la independencia con respecto a variables confusoras, de forma que la inferencia causal solo es aplicable en un ensayo aleatorizado a las diferencias entre-grupos, pero no a las intra-grupo. A pesar de ello, actualmente la mayoría de las revistas científicas de nuestro campo solicitan reportar las diferencias intra-grupo dentro del contexto de un ensayo clínico, un procedimiento que más que ayudar a interpretar mejor los resultados, solo puede confundir y sesgar más al lector, induciendo a malinterpretaciones del ensayo clínico. Por ejemplo, dado que la asignación aleatoria no elimina factores de confusión de las diferencias intra-grupo, donde también influyen aspectos como la historia natural, esto hace que dicha diferencia dentro del grupo experimental tienda a sobreestimar la efectividad de la intervención, ya que en ella también se sumaria el efecto de la historia natural del proceso en cuestión.

A continuación, muestro algunas preguntas frecuentes con sus respectivas respuestas, a fin de prevenir al lector tales malinterpretaciones (algunos aspectos ya se han comentado previamente):

Preguntas y respuestas

Si un grupo experimental mejora de manera significativa y el control no, ¿implica que la intervención es efectiva?

No

Si dos grupos experimentales mejoran igual a lo largo del tiempo, ¿significa que ambas intervenciones son igual de efectivas, o que son efectivas?

No

¿Es necesario tomar una medición basal (antes de aplicar el tratamiento) en un ensayo aleatorizado para evaluar la efectividad de este?

No

Si las diferencias entre grupos no son significativas ni relevantes, pero solo el grupo experimental ha mostrado diferencias significativas intra-grupo, ¿significa que puede que la intervención sea efectiva?

No

¿Calcular la diferencia post- menos basal en un ensayo aleatorizado es un procedimiento estadístico adecuado?

No

¿Las diferencias intra-grupo sobreestiman el efecto de la intervención?

Si

¿Son distintas a nivel conceptual las diferencias entre-grupos ajustadas de un ANCOVA y las calculadas mediante la variable diferencia post- menos basal?

No

¿Es necesario observar las diferencias intra-grupo para interpretar adecuadamente los resultados de un ensayo aleatorizado?

No

 

Literatura de interés

El tema tratado en esta entrada es complejo y con muchos matices y aspectos a tener en consideración, algunos no abordados en la misma. Por ello, recomiendo a cualquier persona interesada en la interpretación y realización de ensayos aleatorizados leer estas fuentes de información a fin de mejorar su entendimiento en esta materia:

Conclusiones

Las diferencias intra-grupo no son necesarias dentro del contexto de un ensayo aleatorizado, pudiendo derivar solo en malinterpretaciones de los resultados del mismo. Por ello, es recomendable no tener en cuenta tales diferencias, incluso no reportarlas, cuando se lea o se realice un estudio con este tipo de diseño. Todo ensayo aleatorizado debería analizarse y reportarse con un modelo ANCOVA (u otra variante de modelo de regresión multivariable, incluyendo la medición basal como covariable).

Asunción de normalidad

•
marzo 4, 2024
•
Modelo Lineal General, Temas Básicos
•
No hay comentarios

Asunciones: Normalidad En esta entrada se recoge una breve explicación de la tan aclamada asunción de normalidad, haciendo hincapié en a que …

Gráficos QQ y PP

•
diciembre 29, 2023
•
Temas Básicos
•
No hay comentarios

Análisis de la "normalidad": Gráficos QQ y PP En esta entrada se recoge una explicación de los gráficos QQ y PP, útiles …

Minima Diferencia Clinicamente Relevante

•
diciembre 9, 2023
•
Temas Básicos
•
No hay comentarios

Interpretación de la relevancia clínica: El mal uso de la mínima diferencia clínicamente relevante (I) En esta entrada se proporciona una breve …

Calculadora Muestral – Ensayo Aleatorizado

•
agosto 8, 2023
•
Calculadora Tamaño Muestral
•
No hay comentarios

Calculadora Muestral: Ensayos Aleatorizados (diferencia ajustada ancova – precisión) En esta entrada se recoge una breve guía práctica de recomendaciones para calcular …

Categorías
Tamaño Muestral Temas Avanzados

Tamaño Muestral: Potencia observada

Tamaño Muestral: Potencia Observada

En esta entrada se recoge una breve explicación del concepto de potencia observada y los motivos por los que esta practica esta totalmente desaconsejada.

La potencia de un determinado análisis estadístico, bajo unas circunstancias determinadas asumidas, sería la probabilidad a largo plazo de obtener un resultado estadísticamente significativo (asumiendo un punto de corte preseleccionado de valor-p) con dicho análisis, siempre y cuando se cumplan todos los supuestos de dichas circunstancias asumidas. En otras palabras, si se cumplen todas las asunciones, y un análisis (ej. t-Student) tiene una potencia del 50% con un tamaño muestral de 40 sujetos por grupo, asumiendo como significativo un valor-p < 0.05, eso significa que si repitiéramos infinitas veces dicho experimento, obtendríamos resultados significativos en el 50% de las replicaciones aproximadamente. Como hemos dicho, todo esto asumiendo que nuestras asunciones se cumplen a la perfección, que en un ejemplo inventado podrían ser:

  • La hipótesis nula (H0) es la diferencia igual a cero.
  • La hipótesis alternativa (H1) especificada es cierta.
  • Diferencia media poblacional bajo la H1 igual a 30.
  • Desviación típica poblacional es igual a 12.
  • Homocedasticidad asumida.
  • Distribución normal asumida.
  • Solo influye el muestreo aleatorio en la variabilidad entre las distintas replicaciones del experimento.

Cualquier variación en estas asunciones alteraría la potencia real de dicho análisis para un determinado tamaño muestral dado.

Muchos investigadores basan sus cálculos de tamaño muestral en la potencia “deseada” para un determinado análisis, partiendo de unas asunciones establecidas a priori. Sin embargo, también hay otra práctica muy extendida, que es el cálculo de la potencia del estudio, una vez se ha realizado el mismo, con los datos obtenidos, conocida como potencia post hoc o potencia observada.

Razones por las que se calcula la potencia observada en investigación

Ejemplo número uno:

Un grupo de investigadores realizan un ensayo aleatorizado con 15 sujetos por grupo, porque eran los que tenían disponibles. Tras ello, obtienen un una diferencia media de 5 puntos (p = 0.011). Sin embargo, como tenían poca muestra, no acaban de estar convencidos de que puedan confiar en esos resultados para rechazar la H0 y aceptar la H1, por ello, deciden calcular la potencia observada del estudio, ya que establecen que si dicha potencia es baja, entonces a lo mejor ese resultado aunque sea significativo, no es una prueba grande en contra de la H0, mientras que si se obtiene una potencia observada alta, eso nos indicaría que podemos confiar más en estos resultados, ya que teníamos muestra suficiente para encontrar dicha diferencia, y por tanto debemos tener más confianza en que podemos rechazar la H0. Realizan el cálculo y obtienen una potencia observada del 73%, concluyendo por tanto que efectivamente, tienen pruebas robustas para rechazar la H0.

Ejemplo número dos:

Otro grupo de investigadores realizan otro ensayo aleatorizado con 15 sujetos por grupo, también porque eran los que tenían disponibles. En este caso, los investigadores obtienen una diferencia media de 2 (p = 0.54). Sin embargo, como tenían poca muestra, deciden calcular la potencia observada, ya que puede ser que ese resultado no sea porque la hipótesis nula es cierta, sino simplemente porque tenían poca potencia para detectar la misma, por el escaso tamaño muestral. De modo que establecen que, si la potencia observada es baja, entonces puede ser simplemente un problema del tamaño muestral, y no de que la H0 sea cierta, y si obtienen una potencia alta, entonces sí que es plausible que los resultados obtenidos se deban a que la H0 es cierta. Obtienen una potencia observada del 9%, concluyendo por tanto que sus resultados posiblemente se deban al pequeño tamaño muestral y no a que la H0 tenga que ser cierta.

Ejemplo número tres: Contraintuitivo

Un tercer grupo de investigadores realizan otro ensayo aleatorizado, en este caso, disponen de 300 sujetos por grupo en su hospital. Obtienen una diferencia media de 1.1 (p = 0.24). Sin embargo, realizan el mismo razonamiento anterior y deciden calcular la potencia observada, resultando en un valor del 22%. Concluyen por tanto que, como la potencia observada es baja, los resultados no se deben en verdad a que la H0 tenga que ser cierta, sino que es un problema de que se tenía poca muestra.

Puede ser que los dos primeros ejemplos pareciesen “razonables”, sin embargo, aplicando ese mismo razonamiento, nos hemos topado con un tercer ejemplo en el que se afirma que una muestra de 300 sujetos por grupo, es también pequeña. De hecho, esto sucedería incluso aunque la muestra hubiera sido de 3000 sujetos por grupo, las conclusiones de dichos investigadores habrían sido las mismas, que la muestra era demasiado pequeña y que dicho valor-p no constituía un indicativo de que la H0 fuese más plausible que la H1.

Relación entre la potencia observada y el valor-p observado

Para poder entender mejor el ejemplo contraintuitivo, así como poder realizar una interpretación adecuada de la potencia observada, es necesario entender su relación con el valor-p observado. En la siguiente figura muestro la relación existente entre el valor-p observado y la potencia observada, para una prueba t-Student para dos muestras independientes.

La potencia observada tiene una relación directa con el valor-p observado, en otras palabras, la potencia observada no aporta información adicional al valor-p observado. Los valores-p pequeños siempre tendrán asociados valores altos de potencia observada y viceversa, sin importar si la H0 es cierta o falsa. De hecho, el gráfico anterior está elaborado con simulaciones donde la H0 es cierta.

Este concepto se puede comprender mejor enfrentando las distribuciones de la H0 y la H1. Por ejemplo, en un caso hipotético de 50 sujetos por grupo, para una potencia del 80%, tendríamos la siguiente figura:

En esta figura, el gráfico de densidad rojo hace referencia a la H0 y el gráfico azul a la H1, el valor de la mitad de alfa (contraste a dos colas) es el umbral crítico de significación (en nuestro caso asumiremos p < 0.05), que se muestra en la figura como una línea verde vertical. La potencia es todo el área bajo la curva azul que queda a la derecha de la línea verde vertical de la derecha, en este caso, el 80%, para una diferencia media observada de 2.85 (desviación estándar = 5). Ahora veamos que pasa si el valor de la diferencia media observada es el que coincide con la línea verde vertical, es decir, el umbral crítico de significación (valor-p = 0.05):

En este caso, la potencia observada es del 50%, ya que como se puede apreciar, la mitad de la gráfica azul queda a la izquierda de la línea verde y la otra mitad a la derecha, por lo que, la probabilidad de obtener un resultado significativo (p < 0.05), sería aproximadamente del 50% asumiendo que la H1 es cierta. Si seguimos desplazando esta gráfica azul a la izquierda, la potencia observada iría disminuyendo progresivamente, y como podemos ver, dado que ambas gráficas son curvilíneas, la relación entre el valor-p observado y la potencia observada no es lineal, sino exponencial como se mostraba en la primera figura. Si nos vamos al extremo, superponiendo las gráficas, puede apreciarse como entonces la potencia observada es igual al umbral crítico de significación especificado, en nuestro caso, 5%.

La potencia observada es engañosa: Llamada a la acción para su abolición

Debido a que la potencia observada tiene una relación directa inversa con el valor-p observado, no sirve para lo que se utiliza en la práctica clínica, como los ejemplos anteriormente mencionados. Si utilizamos la potencia observada para “interpretar mejor” los resultados del valor-p, entonces tenderemos a sobrestimar todos los resultados significativos, porque siempre obtendremos potencias observadas elevadas, y de manera inversa siempre podremos concluir que cualquier resultado no significativo se debe a un escaso tamaño muestral, a expensas de la muestra utilizada, y por tanto la H0 nunca será plausible si así lo deseamos.

Las recomendaciones por estadísticos desde hace décadas es no llevar a cabo dicha práctica, ya que solo deriva en errores de interpretación de los resultados de una investigación. La potencia debería siempre ser establecida a priori, a la hora de realizar el cálculo de tamaño muestral, en función de unas asunciones también establecidas a priori en función de literatura previa y conocimiento técnico sobre la materia, y nunca calculada en base a los resultados del propio estudio. No obstante, aún así mi recomendación sigue siendo, al igual que he especificado en otras entradas de esta web, calcular el tamaño muestral basándonos en la precisión y no en la potencia, que es la metodología adecuada que lleva a menos errores a la larga.

Conclusiones

La potencia post hoc o potencia observada no debe calcularse dentro del seno de una investigación. Este valor no aporta ninguna información adicional al valor-p observado y su cálculo y utilización para interpretar los resultados es engañoso, derivando en errores grandes con respecto a las conclusiones que pueden sacarse del propio estudio.

La potencia debe establecerse siempre a priori en base a unas asunciones también establecidas a priori. Sin embargo, el cálculo de tamaño muestral basado en precisión sigue siendo más recomendado.

Asunción de normalidad

•
marzo 4, 2024
•
Modelo Lineal General, Temas Básicos
•
No hay comentarios

Asunciones: Normalidad En esta entrada se recoge una breve explicación de la tan aclamada asunción de normalidad, haciendo hincapié en a que …

Gráficos QQ y PP

•
diciembre 29, 2023
•
Temas Básicos
•
No hay comentarios

Análisis de la "normalidad": Gráficos QQ y PP En esta entrada se recoge una explicación de los gráficos QQ y PP, útiles …

Minima Diferencia Clinicamente Relevante

•
diciembre 9, 2023
•
Temas Básicos
•
No hay comentarios

Interpretación de la relevancia clínica: El mal uso de la mínima diferencia clínicamente relevante (I) En esta entrada se proporciona una breve …

Calculadora Muestral – Ensayo Aleatorizado

•
agosto 8, 2023
•
Calculadora Tamaño Muestral
•
No hay comentarios

Calculadora Muestral: Ensayos Aleatorizados (diferencia ajustada ancova – precisión) En esta entrada se recoge una breve guía práctica de recomendaciones para calcular …

Categorías
Avanzado Guía Estadística Tamaño Muestral Temas Avanzados

Tamaño Muestral ANOVA mixto GPower

Tamaño muestral: NOTA SOBRE TAMAÑOS DEL EFECTO EN ANOVAS DE MEDIDAS REPETIDAS con G*Power

En esta entrada se recoge una breve explicación de uno de los errores más comunes cometidos dentro del campo de la Fisioterapia, a la hora de calcular tamaños muestrales con el programa G*Power.

El software G*Power es uno de los más utilizados dentro del campo de la Fisioterapia (y otros) para calcular tamaños muestrales a priori durante la fase de planificación de un estudio de investigación. Este software facilita cálculos de tamaño muestral basados en potencia para distintos análisis, como comparaciones de dos medias, correlación de Pearson y lo que es la temática de esta entrada, los Análisis de la Varianza (ANOVA), más concretamente aquellos con medidas repetidas.
Desde aquí y en el resto de la entrada, basaré las explicaciones en un ANOVA mixto con tres grupos de tratamiento (ejercicio, terapia manual, vendaje) y 4 momentos de medición (basal, 3 meses, 6 meses y 12 meses), ya que es el tipo de análisis que suele usarse para calcular tamaños muestrales en ensayos controlados aleatorizados en Fisioterapia. Los cálculos propuestos son para la interacción tiempo-por-grupo.

Comenzaré con un pequeño ejemplo de cómo se suele proceder en G*Power para calcular ese tamaño muestral a priori. Para poder calcularlo se requiere especificar una serie de valores:

  • Número de grupos.
  • Número de mediciones.
  • Tamaño del efecto estimado (f o ηp2).
  • Correlación entre medidas repetidas.
  • Potencia deseada.
  • Nivel alfa de significación.
  • Corrección en caso de no esfericidad.

De estos datos, ya tenemos especificados algunos en base al diseño que he propuesto, y otros los asumiremos según valores típicos utilizados en Fisioterapia:

  • Número de grupos: 3
  • Número de mediciones: 4
  • Tamaño del efecto: Medio (f = 0.25 // ηp2 = 0.06)
  • Correlación entre medidas repetidas: 0.50
  • Potencia deseada: 80%
  • Nivel alfa de significación: 0.05
  • Corrección en caso de no esfericidad: Sin corrección (igual a 1)

Con estos datos, el tamaño muestral calculado es de 30 sujetos, es decir, 10 sujetos por grupo. Parece algo pequeño, pero…si el G*Power nos ha dado ese resultado, es que es correcto, ¿o no? A continuación, explicaré con más detalle el punto sobre el que trata la entrada, el tamaño el efecto, y haré un pequeño matiz al final de esta sobre la asunción de esfericidad asumida.

Tamaños del efecto pequeños, medios y grandes. Dos etas cuadrado

En el anterior ejemplo he especificado que se estimaba un tamaño del efecto medio, que se correspondía con un valor f = 0.25 o un valor de ηp2 = 0.06. Estos valores no los he nombrado al azar, ya que mucha gente se basa en la siguiente recomendación sobre lo que es un tamaño del efecto pequeño, medio y grande en el caso de ANOVAs:

  • Efecto pequeño: f = 0.10 / ηp2 = 0.01
  • Efecto medio: f = 0.25 / ηp2 = 0.06
  • Efecto grande: f = 0.40 / ηp2 = 0.14

Con respecto a los ANOVA, hay distintos tamaños del efecto, me centraré solamente en dos para esta entrada: el coeficiente eta cuadrado (η2) y el coeficiente eta cuadrado parcial (ηp2). El primero se usaría cuando solo tenemos un factor (ej., comparamos 3 grupos con una sola medición, solo habría un factor, el factor grupo). El segundo por su lado, se utiliza cuando tenemos varios factores, como sería en nuestro ejemplo de ensayo aleatorizado, donde disponemos del factor grupo y el factor tiempo (medidas repetidas). De forma simplificada, pueden definirse matemáticamente como:

$$\eta^2 = \frac{SS_{efecto}}{SS_{total}}$$

$$\eta_{p}^2 = \frac{SS_{efecto}}{SS_{efecto} + SS_{error}}$$

En el caso de un ANOVA mixto, tenemos 3 posibles efectos de interés, el efecto principal grupo, el efecto principal tiempo y la interacción tiempo por grupo. De este modo, si nuestro interés es la interacción tiempo-por-grupo, tendríamos (nota: fórmulas simplificadas):

$$\eta^2 = \frac{SS_{interaccion}}{SS_{interaccion} + SS_{grupo} + SS_{tiempo} + SS_{error}}$$

$$\eta_{p}^2 = \frac{SS_{interaccion}}{SS_{interaccion} + SS_{error}}$$

Eta cuadrado parcial y correlación entre medidas repetidas

El coeficiente eta cuadrado parcial (ηp2) se ve influenciado por la correlación entre medidas repetidas. No entraré en detalles, pero esa influencia es en el sentido de que, a mayor correlación entre medidas repetidas, mayor valor de ηp2 y consecuentemente, mayor potencia estadística (es decir, se requerirá menor muestra). Por ejemplo, imaginemos el caso anterior, con una correlación asumida de 0.50 el tamaño muestral resultante era de 30 sujetos. Si elevamos la correlación asumida a 0.70, el tamaño muestral baja a 21 sujetos, y si la elevamos a 0.90, entonces el cálculo nos devuelve tan solo 9 sujetos (3 por grupo).

Sobra decir que manipular dicha correlación para obtener un menor tamaño muestral es engañoso. En ausencia de datos previos, lo ideal sería asumir una correlación de 0.50 como máximo, o ser incluso más conservadores con correlaciones más pequeñas si las mediciones están muy separadas en el tiempo (de 0.40-0.45 por ejemplo) (Walters 2019). Asumir correlaciones por encima de 0.50 debe estar muy justificado.

Distintos tamaños del efecto: EL ERROR
Todas las explicaciones anteriores enlazan con este apartado, que es el verdadero motivo de la entrada, la existencia de distintas especificaciones de tamaño del efecto f y ηp2, que pueden llevar a cometer errores importantes al realizar cálculos de tamaño muestral con G*Power. Tenemos tres métodos:
  • Método que usa G*Power.
  • Método basado en datos extraídos de SPSS.
  • Método basado en Cohen, 1988 (quién dio las recomendaciones de tamaño del efecto mencionadas anteriormente).
La diferencia entre ellos es la utilización de la correlación de medidas repetidas. Utilizando el método que aparece por defecto en G*Power, debemos especificar la correlación para el cálculo del tamaño muestral. Esto se debe a que G*Power no tiene en cuenta dicha correlación para la especificación del tamaño del efecto estimado que le hemos especificado, sino que la utiliza luego directamente en el cálculo. Por otro lado, cuando se calcula en SPSS un coeficiente eta cuadrado parcial (ηp2), se tiene en cuenta ya para su cálculo la correlación entre medidas repetidas. En otras palabras, el coeficiente eta cuadrado parcial en que se basa el cálculo de G*Power, no es el mismo que el que facilita SPSS, sus valores no coinciden, así como tampoco es lo mismo un f = 0.25 según G*Power, que un f = 0.25 según SPSS, tal y como se especifica en el manual de utilización del G*Power. Anteriormente he comentado que a mayor correlación mayor valor de ηp2 y, por tanto, menos muestra necesaria para un determinado estudio, como mostré incrementando la correlación en el cálculo inicial. Por otro lado, como acabo de comentar, el cálculo del coeficiente ηp2 que facilita SPSS al hacer un análisis, ya tiene en cuenta la correlación entre medidas repetidas. Por tanto, si nos basamos en un ηp2 de SPSS, que ya tiene en cuenta dicha correlación y por tanto será más grande, y lo metemos en el G*Power para calcular el tamaño muestral según G*Power, donde tenemos que especificar la correlación, estamos usando dos veces la correlación, una vez que se usó en SPSS para dar el valor de ηp2 y otra ahora en el cálculo del tamaño muestral en G*Power, con la implicación de que sobreestimamos el tamaño del efecto y por consecuente, infraestimamos la muestra necesaria. Existe una opción en el G*Power para especificar al software en que nos estamos basando cuando especificamos un tamaño del efecto para calcular el tamaño muestral basado en un ANOVA con medidas repetidas, abajo del todo en un botón de “Opciones”.
Es imprescindible cambiar en dicho apartado la especificación del tamaño del efecto según en que nos estemos basando. Si nos basamos en datos extraídos de estudios previos, que por lo general utilizan la forma de cálculo de ηp2 del SPSS donde ya se tiene en cuenta la correlación entre medidas repetidas, debemos seleccionar dicho apartado en “Opciones”. Mientras que, si nos basamos en las “recomendaciones de Cohen” de un tamaño pequeño, medio y grande, entonces debemos seleccionar dicha opción. ¿Por qué es tan importante esto? Volviendo al ejemplo inicial, nos salía una muestra de 30 sujetos (10 por grupo), para un supuesto valor f = 0.25, siguiendo las recomendaciones de que ese valor corresponde a un tamaño del efecto medio según Cohen. Si ahora especificamos que el tamaño del efecto es según Cohen en la pestaña “Opciones”, el tamaño muestral resultante es de 222 sujetos (74 sujetos por grupo). Veamos otro ejemplo con valores reales extraídos de un reciente estudio. En este estudio se calcula el tamaño muestral para la interacción tiempo-por-grupo de un ANOVA mixto con las siguientes especificaciones:
  • Número de grupos: 4
  • Número de mediciones: 3
  • Tamaño del efecto: ηp2 = 0.048 (extraído de un estudio piloto previo, calculado con SPSS).
  • Correlación entre medidas repetidas: 0.50
  • Potencia deseada: 90%
  • Nivel alfa de significación: 0.01
  • Corrección en caso de no esfericidad: Sin corrección (igual a 1)
De acuerdo con sus especificaciones, el tamaño muestral resultante reportado en el estudio fue de 84 sujetos (21 por grupo). Este sería el tamaño muestral calculado, basándose en un ηp2 de 0.048 extraído de SPSS, pero manteniendo la especificación de tamaño del efecto según G*Power. Al cambiar en la pestaña “Opciones” el tamaño del efecto a “según SPSS”, el tamaño muestral resultante es de 240 sujetos (60 por grupo). Es decir, su estudio con esa muestra no “tenía” una potencia como ellos querían del 90%, sino que realmente tenía una potencia del 28%, por haber especificado mal el tamaño del efecto en G*Power a la hora de realizar su cálculo.
Una nota sobre la esfericidad

No entraré en detalles en esta entrada acerca de la asunción de esfericidad, ya que no es el propósito de esta. Pero si quisiera hacer una anotación de cara a los cálculos de tamaño muestral basados en ANOVA mediante G*Power. De manera resumida, la asunción de esfericidad rara vez (por no decir nunca) podemos asumir que se cumpla en la vida real. Esto implica que no podemos especificar valores de corrección iguales a 1, es decir, sin corrección, asumiendo que dicho asunción se cumplirá a la perfección. La opción correcta es asumir un cierto grado de incumplimiento en dicha asunción, y tener en cuenta este aspecto para calcular el tamaño muestral, introduciendo una ligera corrección. Si no disponemos de datos previos fiables, una opción conservadora es establecer un valor de corrección de esfericidad de 0.75. ¿Por qué es esto importante?

Cuando la asunción de esfericidad se cumple a la perfección (corrección igual a 1) se requiere menos muestra para encontrar un efecto. En otras palabras, si ponemos el valor de 1 en el cálculo, obtendremos menos muestra. Pero como he comentado, esta situación es muy poco plausible en la vida real, de modo que, si hacemos eso, estaríamos infraestimando nuestra muestra.

En los ejemplos anteriormente mencionados, la muestra del primer estudio inventado (especificando bien el tamaño del efecto) pasaría de 222 sin corrección, a 267 sujetos con una corrección de 0.75. En el segundo caso del estudio real, el cambio sería de 240 sin corrección, a 292 sujetos con la corrección de 0.75.

Precisión por encima de potencia

El contenido de esta entrada tiene como objetivo simplemente explicar algunos errores comunes realizados al calcular tamaños del efecto basados en potencia con G*Power. No obstante, nada del contenido de la misma debe ser interpretado como una recomendación a favor de los cálculos de tamaño muestral basados en potencia, que tienden a infraestimar las muestras necesarias en investigación. Mi recomendación es basar siempre los cálculos en la precisión en lugar de la potencia. En el apartado de Repositorio: Guías de Estadística, se recogen distintas fuentes de información para realizar cálculos de tamaño muestral adecuadamente para distintos tipos de análisis.

Conclusiones

Por lo general, dentro del campo de la investigación en Fisioterapia, se utilizan muestras demasiado pequeñas en la mayoría de estudios publicados. Los principales motivos que achaco a este fenómeno son: 1) Cálculos basados en potencia y no precisión; 2) asunción de cumplimiento de distintas asunciones estadísticas que no se cumplen en realidad; 3) utilización errónea de la algunas herramientas disponibles para cálculos de tamaño muestral (como el G*Power); y 4) ausencia de adherencia a las recomendaciones de expertos en la materia.

La investigación en Fisioterapia se vería beneficiada enormemente por una mejora en las estimaciones a priori de tamaños muestrales basados en precisión, con la utilización correcta de las distintas herramientas disponibles, y adhiriéndose a las recomendaciones de expertos en la materia para un determinado tipo de diseño y/o análisis estadístico.

Asunción de normalidad

•
marzo 4, 2024
•
Modelo Lineal General, Temas Básicos
•
No hay comentarios

Asunciones: Normalidad En esta entrada se recoge una breve explicación de la tan aclamada asunción de normalidad, haciendo hincapié en a que …

Gráficos QQ y PP

•
diciembre 29, 2023
•
Temas Básicos
•
No hay comentarios

Análisis de la "normalidad": Gráficos QQ y PP En esta entrada se recoge una explicación de los gráficos QQ y PP, útiles …

Minima Diferencia Clinicamente Relevante

•
diciembre 9, 2023
•
Temas Básicos
•
No hay comentarios

Interpretación de la relevancia clínica: El mal uso de la mínima diferencia clínicamente relevante (I) En esta entrada se proporciona una breve …

Calculadora Muestral – Ensayo Aleatorizado

•
agosto 8, 2023
•
Calculadora Tamaño Muestral
•
No hay comentarios

Calculadora Muestral: Ensayos Aleatorizados (diferencia ajustada ancova – precisión) En esta entrada se recoge una breve guía práctica de recomendaciones para calcular …

Categorías
Guía Estadística Repositorio Tamaño Muestral

Tamaño Muestral Modelos Predictivos

repositorio: tamaño muestral modelos predictivos

Minimum sample size for developing a multivariable prediction model: Part I – Continuous outcomes | Stat Med

  • En este artículo se ofrece una guía de cálculo de tamaño muestral mínimo para la elaboración de modelos predictivos multivariables cuando la variable resultado es continua.

Minimum sample size for developing a multivariable prediction model: PART II – binary and time-to-event outcomes | Stat Med (Acceso libre)

  • En este artículo se ofrece una guía de cálculo de tamaño muestral mínimo para la elaboración de modelos predictivos multivariables cuando la variable resultado es dicotómica o el tiempo de supervivencia.

Minimum sample size calculations for external validation of a clinical prediction model with a time-to-event outcome | Stat Med (Acceso libre)

  • En este artículo se ofrecen recomendaciones de cálculo de tamaño muestral mínimo para la validación externa de un modelo predictivo multivariable cuando la variable resultado es el tiempo de supervivencia.

Minimum sample size for external validation of a clinical prediction model with a binary outcome | Stat Med (Acceso libre)

  • En este artículo se ofrecen recomendaciones de cálculo de tamaño muestral mínimo para la validación externa de un modelo predictivo multivariable cuando la variable resultado es dicotómica.

Calculating the sample size required for developing a clinical prediction model | BMJ (Acceso libre)

  • En este artículo se recogen tres guías de cálculo de tamaño muestral mínimo para la elaboración de modelos predictivos multivariables con variables resultado continuas, dicotómicas y de tiempo de supervivencia, incluyendo ejemplos de los cálculos y recomendaciones de qué hacer cuando no se dispone de algunos datos de investigaciones previas.

A note on estimating the Cox-Snell R2 from a reported C statistic (AUROC) to inform sample size calculations for developing a prediction model with a binary outcome | Stat Med (Acceso libre)

  • En este artículo se ofrece una guía de como estimar el coeficiente R2 de Cox-Snell en función del estadístico C para realizar cálculos de tamaño muestral para la elaboración de modelos predictivos con una variable resultado dicotómica

Paquete de R ‘pmsampsize’

  • En este enlace se recoge la documentación disponible con respecto al paquete de R ‘pmsampsize’ con el que se puede realizar el cálculo de tamaño muestral mínimo para la elaboración de modelos predictivos con variables resultado continuas, dicotómicas y de tiempo de supervivencia. Este paquete implementa los conocimientos de los artículos mencionados anteriormente para dichos cálculos, facilitando la tarea.

Aplicación Web basada en ‘pmsampsize’

  • Esta aplicación hace los mismos cálculos que el paquete de R ‘pmsampsize’, para aquellos que estén familiarizados con el programa. La guía para su utilización se recoge aquí.

Asunción de normalidad

•
marzo 4, 2024
•
Modelo Lineal General, Temas Básicos
•
No hay comentarios

Asunciones: Normalidad En esta entrada se recoge una breve explicación de la tan aclamada asunción de normalidad, haciendo hincapié en a que …

Gráficos QQ y PP

•
diciembre 29, 2023
•
Temas Básicos
•
No hay comentarios

Análisis de la "normalidad": Gráficos QQ y PP En esta entrada se recoge una explicación de los gráficos QQ y PP, útiles …

Minima Diferencia Clinicamente Relevante

•
diciembre 9, 2023
•
Temas Básicos
•
No hay comentarios

Interpretación de la relevancia clínica: El mal uso de la mínima diferencia clínicamente relevante (I) En esta entrada se proporciona una breve …

Calculadora Muestral – Ensayo Aleatorizado

•
agosto 8, 2023
•
Calculadora Tamaño Muestral
•
No hay comentarios

Calculadora Muestral: Ensayos Aleatorizados (diferencia ajustada ancova – precisión) En esta entrada se recoge una breve guía práctica de recomendaciones para calcular …

Categorías
Análisis Crítico Modelo Lineal General Observacional

Análisis Crítico #1

Prediction equation of hip external rotators maximum torque in healthy adults and older adults using the measure of hip extensors maximum torque: Análisis Crítico

Abstract

  • Background

    The use of predictive equation of muscular torque can reduce physical effort and time spent during evaluation. The aim of this study is to establish, validate, and test the accuracy of a prediction equation to estimate the hip external rotators (HER) torque in adults and older adults by means of hip extensors (HEX) torque measurement.

  • Design

    Cross-sectional.

  • Methods

    Eighty-three healthy adults (development set) were assessed to test the association of HEX and HER torques and to establish the prediction equation. A separate 36 adults and 15 older adults (validation sets) were assessed to test the ability of the equation to estimate HER torque. Hip isometric strength was assessed by a handheld dynamometer.

  • Results

    Simple linear regression analysis revealed that HEX torque was associated with HER torque (r = 0.80; p < 0.0001), resulting in the following prediction equation: HERtorque= −0.02 + (0.58 * HEXtorque). Paired t-test revealed no difference between directly measured and predicted values of HER torque in adults (mean difference = 0.02; 95% CI = −0.115, 0.072) and older adults (mean difference = 0.05; 95% CI = −0.02, 0.12).

  • Conclusion

    Simple linear regression analysis revealed that HEX torque was associated with HER torque (r = 0.80; p < 0.0001), resulting in the following prediction equation: HERtorque= −0.02 + (0.58 * HEXtorque). Paired t-test revealed no difference between directly measured and predicted values of HER torque in adults (mean difference = 0.02; 95% CI = −0.115, 0.072) and older adults (mean difference = 0.05; 95% CI = −0.02, 0.12).

Enlace

https://doi.org/10.1016/j.bjpt.2020.08.005

Carta de respuesta al editor

https://doi.org/10.1016/j.bjpt.2023.100515

Carta de respuesta de los autores

https://doi.org/10.1016/j.bjpt.2023.100516

Categorías
Modelo Lineal General Temas Básicos

Transitividad de Correlaciones

Correlación: Transitividad

En esta entrada se explica la transitividad del coeficiente de correlación de Pearson, así como la malinterpretación común que suele hacerse sobre dicha propiedad, pudiendo llevar a conclusiones erróneas.

Antes de comenzar la lectura de esta entrada, me gustaría pedirte que realizases el siguiente test, que se repetirá de manera similar al final de la entrada, con el objetivo de que puedas darte cuenta las creencias erróneas que tienes actualmente y de si has adquirido conocimientos nuevos tras la lectura de la entrada.

41
Creado en Por Admin

Transitividad Correlaciones (Test Inicial)

1 / 9

Solo cuando la correlación entre X e Y y la correlación entre Z e Y tienen signos opuestos, puede ser cero la correlación entre X y Z.

2 / 9

Podemos tener dos variables X e Y que presenten un coeficiente de correlación de Pearson de 0.70, y otras dos variables Z e Y que presenten también una correlación de Pearson de 0.70, siendo la correlación entre X y Z igual a cero.

3 / 9

Si la correlación entre dos variables X e Y es de -0.40, y la correlación entre Z e Y es de 0.40, entonces si o si la correlación entre X y Z será igual a cero.

4 / 9

Si una variable X presenta una correlación de 0.90 con otra variable Y, y dicha variable Y presenta una correlación de 0.40 con otra variable Z, la correlación entre X y Z será positiva y mayor de 0.40.

5 / 9

Si la correlación entre dos variables X e Y es de r-1, y la correlación entre Z e Y es de r-2, entonces la correlación entre X y Z estará comprendida entre [r-1, r-2].

6 / 9

Si una variable X presenta una correlación negativa con otra variable Y, y dicha variable Y presenta una correlación negativa con otra variable Z, entonces la correlación entre X y Z será positiva.

7 / 9

Si una variable X se correlaciona (positiva o negativamente) con una variable Y, y dicha variable Y se correlaciona (positiva o negativamente) con otra variable Z, entonces si o si, deberá existir una correlación (positiva o negativa) entre X y Z.

8 / 9

Si una variable X presenta una correlación positiva con otra variable Y, y dicha variable Y presenta una correlación negativa con otra variable Z, entonces la correlación entre X y Z será negativa.

9 / 9

Si una variable X presenta una correlación positiva con otra variable Y, y dicha variable Y presenta a su vez una correlación positiva con otra variable Z, entonces la correlación entre X y Z será también positiva.

Tu puntación es

The average score is 68%

LinkedIn Facebook Twitter VKontakte
0%

Imaginemos que sabemos que existe una relación entre la fuerza de prensión manual máxima (X) y la fuerza en rotación externa isométrica máxima de hombro (Y), y que existe una relación entre dicha rotación externa isométrica máxima (Y) y la discapacidad del hombro (Z). En base a ello, decidimos empezar a usar la fuerza de prensión manual como estimador de la discapacidad del hombro. En este razonamiento estaríamos haciendo uso de la transitividad, como X se relaciona con Y, y Y se relaciona con Z, entonces X se relaciona con Z, es decir, hay una «transmisión de la correlación».

Para poder entender la transitividad aplicada a las correlaciones, debemos conocer antes el concepto del coeficiente de determinación (R2) y el porcentaje de variabilidad explicada. A modo resumen simple, en función del valor del coeficiente de correlación de Pearson (r):

  • r = 0, no hay correlación.
  • r = 1, correlación perfecta positiva.
  • r = -1, correlación perfecta negativa.

Si elevamos dicho coeficiente de correlación al cuadrado, obtenemos el coeficiente de determinación (R2), que indica el porcentaje de variabilidad que podemos explicar de una variable a través de otra, por ejemplo si tenemos un coeficiente de Pearson de 0.50, el coeficiente de determinación sería R2 = 0.25, es decir, un 25% de variabilidad explicada. Este concepto puede representarse gráficamente con diagramas de Venn, que facilitarán entender el concepto de transitividad de las correlaciones. Si el área de ambos rectángulos es de 1, un R2 de 0.25 implica que hay un solapamiento del 25% del área los rectángulos.

Imaginemos ahora que tenemos tres variables en lugar de dos, con los siguientes valores de R2 entre ellas:

  • X-Y: 0.25
  • Y-Z: 0.25

Una posible representación mediante diagramas de Venn de estos valores de R2 sería la siguiente:

Cómo se puede apreciar en dicho diagrama, a pesar de que hay una correlación (r = 0.50) entre X e Y y Z e Y, los rectángulos de X y Z no se solapan, indicando una ausencia de correlación entre ellas. En otras palabras, que dos variables (X y Z) se relacionen con una misma variable (Y), no implica que esas dos tengan que presentar una correlación. Este es el principal error de interpretación que se comete con respecto a la transitividad de las correlaciones. Volviendo al ejemplo inicial sobre la prensión manual, la información facilitada en dicho enunciado impide saber si realmente la prensión manual se relaciona con la discapacidad del hombro, se requieren más datos. Pero… ¿Qué datos?

Tenemos dos opciones, una buena y adecuada y otra mala que solo utilizaré para ejemplificar la propiedad de transitividad aplicada a las correlaciones. La opción buena es la obvia, si se quiere estimar la correlación entre dos variables, lo adecuado es medir ambas y analizar directamente dicha correlación, no hacer estimaciones indirectas basadas en la transitividad.

Como ya he comentado, no tiene porque haber transitividad de una correlación de Pearson. Sabemos que la correlación entre X y Z se encuentra dentro del siguiente intervalo basado en las correlaciones entre X e Y y Z e Y:

$$r_{xy}r_{yz} – \sqrt{(1- R^2_{xy})(1-R^2_{yz})} \leq r_{xz} \leq r_{xy}r_{yz} + \sqrt{(1- R^2_{xy})(1-R^2_{yz})}$$

De esta fórmula podemos extraer varias conclusiones. Una primera es que, si y solo si rxy = ryz = 0, entonces rxz puede tomar todo el rango de valores posibles, es decir, de -1 a +1.

Otra conclusión sería que, si y solo si rxy = ryz (sin tener en cuenta el signo de la correlación, es decir, su valor absoluto), entonces puede existir una correlación perfecta entre X y Z, es decir rxz = 1 o rxz = -1, cuyo signo dependerá de los de las otras dos relaciones. Si nos imaginamos esta situación con los diagramas de Venn, tiene más sentido, pues que haya una relación perfecta (positiva o negativa) entre X y Z, implica que ambos rectángulos estarían superpuestos de manera perfecta y por tanto, el solapamiento de ambos con la variable Y sería el mismo, es decir, R2xy = R2yz.

Por otro lado y aunque no tan fácilmente reconocible como esa primera conclusión, de dicha fórmula también podemos concluir que, si rxy > 0, y ryz > 0, entonces rxz > 0 si y solo si:

$$R^2{xy} + R^2{yz} > 1$$

Es decir, habría transitividad de la correlación positiva solo cuando se cumpla esa situación. De forma más generalista, solo cuando la anterior situación se cumpla, la correlación entre X y Z no podrá ser igual a cero, en el resto de casos, puede existir una correlación igual a cero entre ambas variables. Nuevamente, si pensamos en los diagramas de Venn, podemos apreciar esa condición más fácilmente. El área del rectángulo de Y es igual a 1, de manera que si la suma de las áreas solapadas de X y Z con Y son superiores a 1, eso implica que los rectángulos de X y Z han de estar solapados también. A continuación muestro un ejemplo de diagrama de Venn donde casi hay solapamiento entre X y Z, con solo un 5% de la variabilidad de Y sin explicar. Si X y Z explicasen más porcentaje de la variabilidad de Y, es decir, si juntásemos más dichos rectángulos, acabarían por solaparse.

Este punto es importante, pues incluso con correlaciones altas  entre X e Y y Z e Y, puede darse una correlación de cero entre X y Z. Por ejemplo, asumiendo que rxy = ryz, entonces la correlación máxima que permitiría la posibilidad de que existiera una correlación de cero entre X y Z sería:

$$r_{xy} = r_{yz} = \sqrt 50 = 0. 7071$$

Es decir, podemos tener hasta una correlación entre X e Y y entre Z e Y de 0.7071 y ello no tendría que implicar que hubiera una correlación entre X y Z. Con la fórmula inicial de los intervalos del coeficiente de correlación entre X y Z en función de rxy y ryz, podemos calcular la correlación mínima que podríamos esperar entre X y Z, así como también evaluar en que situaciones es plausible una ausencia de correlación entre ambas variables.

Implicaciones de la malinterpretación de la transitividad de las correlaciones

¿Por qué es importante conocer como se comportan las correlaciones con respecto a la transitividad? Para no cometer errores grandes y, en mi experiencia por lo que he podido apreciar, encadenados, de interpretaciones y asunciones. Un ejemplo de malinterpretación común sería el siguiente:

«Estamos buscando artículos y nos encontramos con uno que ha visto que hay una correlación de 0.7 entre la fuerza máxima prensil y la fuerza isométrica máxima de rotación externa de hombro, nos acordamos que hace unos meses leímos otro estudio que había encontrado una correlación de 0.67 entre la fuerza isométrica máxima de rotación externa y la discapacidad del hombro, y en base a ambos estudios, decidimos empezar a evaluar y tratar la fuerza prensil en clínica en sujetos con patología dolorosa del hombro.»

Otra opción sería que, en función de esos dos estudios, decidiéramos hacer un ensayo clínico orientado a trabajar la fuerza prensil para mejorar la discapacidad en sujetos con dolor relacionado con el manguito rotador, o que decidiéramos no evaluar en un transversal la fuerza de rotación externa porque requiere de un dinamómetro que es más caro y midiéramos en su lugar la fuerza prensil, asumiendo que también se relaciona con la discapacidad. Todas estas decisiones son erróneas y pueden llevar a errores muy grandes, tanto en la práctica clínica como en investigación. Cuando he comentado que en mi experiencia, son errores encadenados, es porque muchas veces he observado que, en lugar de molestarnos en evaluar directamente las correlaciones, las asumimos presentes por transitividad, una tras otra, aceptando algunas como verdades ya comprobadas, y guiando líneas de investigación durante años y años, en base a un error conceptual de estadística.

Por último, otro ejemplo donde también aprecio se malinterpreta notoriamente la transitividad es en las pruebas de valoración. Tendemos a buscar métodos más baratos para evaluar determinados parámetros en nuestros sujetos en investigación, porque se supone tendrán mayor aplicabilidad clínica. Si bien esto es lo deseable, no siempre es posible. En esta búsqueda de métodos más baratos, pecamos de la falacia de la transitividad. Cuando se realiza un estudio de estas características, se suele comparar el nuevo método con uno considerado «gold standard» para evaluar su validez, calculándose la correlación entre las mediciones tomadas con ambos métodos. Mucha gente asume que por ejemplo, un valor de correlación de Pearson de 0.70, sería indicativo de buena validez, y concluyen que por tanto, el nuevo método podría implementarse en la práctica clínica e investigación, ahorrando costes. El motivo subyacente en la gran mayoría de casos, sea consciente o no quien realiza el mismo, es la aceptación de la transitividad, mejor dicho, la malinterpretación de la misma.

Si aceptamos una correlación de 0.70 entre ambos métodos de medición, necesitaríamos que se diera una correlación de 0.72 entre el gold standard y otra variable de interés, para que empezase a haber transitividad de dicha correlación hacia el nuevo método de medición. Por ejemplo, si asumimos que el gold standard presenta una correlación de 0.85 con otra variable, la correlación estimada del nuevo método de medición con dicha variable, por transitividad, sería de 0.219. ¿Podemos por tanto usar indistintamente el nuevo método de medición? La respuesta es, en función de solo esta información, no. Pues ya hemos visto que la transitividad no justificaría dejar de usar el gold standard, pues perderíamos casi toda la correlación con la otra variable de interés. Esto no implica que no pudiera darse una relación más alta entre el nuevo método y dicha variable, simplemente que, por transitividad, no pasaría y por tanto un razonamiento basado en la misma, no se sostiene.

A continuación te dejo un segundo test, con el fin de que puedas evaluar el conocimiento que has adquirido con la presente entrada y si ha mejorado tu capacidad de interpretación de literatura científica:

8
Creado en Por Admin

Transitividad Correlación (Test Final)

1 / 15

Si una variable X presenta una correlación de 0.90 con otra variable Y, y dicha variable Y presenta una correlación de 0.40 con otra variable Z, la correlación entre X y Z será positiva y mayor de 0.40.

2 / 15

Solo cuando la correlación entre X e Y y la correlación entre Z e Y tienen signos opuestos, puede ser cero la correlación entre X y Z.

3 / 15

Dadas tres variables (X, Y, Z), si la correlación entre X e Y es de 0.50 y la correlación entre Z e Y es de 0.49, ¿Puede la correlación entre X y Z llegar a ser perfecta (sin importar el signo)?

4 / 15

Si una variable X presenta una correlación positiva con otra variable Y, y dicha variable Y presenta a su vez una correlación positiva con otra variable Z, entonces la correlación entre X y Z será también positiva.

5 / 15

Dadas tres variables (X, Y, Z), si la correlación entre X e Y es de 0.80, ¿Cuál es la correlación mínima que tendría que haber entre Z e Y para que hubiera transitividad hacia la correlación entre X y Z?

6 / 15

Si la correlación entre la fuerza prensil y la fuerza en rotación externa de hombro es de 0.60, y la correlación entre la fuerza en rotación externa y la discapacidad es de 0.50, ¿Cuáles serían los límites de posibles valores de la correlación entre la prensión manual y la discapacidad?

7 / 15

Si la correlación entre dos variables X e Y es de -0.40, y la correlación entre Z e Y es de 0.40, entonces si o si la correlación entre X y Z será igual a cero.

8 / 15

Si la correlación entre dos variables X e Y es de r-1, y la correlación entre Z e Y es de r-2, entonces la correlación entre X y Z estará comprendida entre [r-1, r-2].

9 / 15

Dadas tres variables (X, Y, Z), sabiendo que la correlación entre X e Y es de 0.60 y la correlación entre Z e Y es de 0.70. ¿Podría haber una correlación entre X y Z igual a cero?

10 / 15

Si una variable X presenta una correlación negativa con otra variable Y, y dicha variable Y presenta una correlación negativa con otra variable Z, entonces la correlación entre X y Z será positiva.

11 / 15

Si la correlación entre la fuerza en rotación externa máxima de hombro y el grado de discapacidad es de 0.60, y la correlación entre dicha fuerza en rotación externa y la fuerza prensil es de 0.90, ¿Cuál es la correlación estimada por transitividad entre la fuerza prensil y la discapacidad de hombro?

12 / 15

Dadas tres variables (X, Y, Z), si la correlación entre X e Y es de 0.40 y la correlación entre Z e Y es de 0.80, ¿Puede ser negativa la correlación entre X y Z?

13 / 15

Podemos tener dos variables X e Y que presenten un coeficiente de correlación de Pearson de 0.70, y otras dos variables Z e Y que presenten también una correlación de Pearson de 0.70, siendo la correlación entre X y Z igual a cero.

14 / 15

Si una variable X se correlaciona (positiva o negativamente) con una variable Y, y dicha variable Y se correlaciona (positiva o negativamente) con otra variable Z, entonces si o si, deberá existir una correlación (positiva o negativa) entre X y Z.

15 / 15

Si una variable X presenta una correlación positiva con otra variable Y, y dicha variable Y presenta una correlación negativa con otra variable Z, entonces la correlación entre X y Z será negativa.

Tu puntación es

The average score is 69%

LinkedIn Facebook Twitter VKontakte
0%

Conclusiones

Las correlaciones no son transitivas, la posibilidad de presencia o no de transitividad depende de la magnitud y dirección de las correlaciones. No debemos caer en el error de inferir asociaciones por transitividad, sin haberlas evaluado de manera directa, pues puede llevarnos a cometer errores cruciales tanto en investigación, como en la práctica clínica.

Asunción de normalidad

•
marzo 4, 2024
•
Modelo Lineal General, Temas Básicos
•
No hay comentarios

Asunciones: Normalidad En esta entrada se recoge una breve explicación de la tan aclamada asunción de normalidad, haciendo hincapié en a que …

Gráficos QQ y PP

•
diciembre 29, 2023
•
Temas Básicos
•
No hay comentarios

Análisis de la "normalidad": Gráficos QQ y PP En esta entrada se recoge una explicación de los gráficos QQ y PP, útiles …

Minima Diferencia Clinicamente Relevante

•
diciembre 9, 2023
•
Temas Básicos
•
No hay comentarios

Interpretación de la relevancia clínica: El mal uso de la mínima diferencia clínicamente relevante (I) En esta entrada se proporciona una breve …

Calculadora Muestral – Ensayo Aleatorizado

•
agosto 8, 2023
•
Calculadora Tamaño Muestral
•
No hay comentarios

Calculadora Muestral: Ensayos Aleatorizados (diferencia ajustada ancova – precisión) En esta entrada se recoge una breve guía práctica de recomendaciones para calcular …