Ensayos aleatorizados: Cambio intra- & entre-grupos
En esta entrada se recoge una breve explicación de los cambios intra-grupos y entre-grupos dentro del contexto de un ensayo aleatorizado, haciendo hincapié en su finalidad, limitaciones y adecuada interpretación.
De la práctica clínica a los ensayos aleatorizados
En la práctica clínica, la forma que disponemos de saber si un paciente mejora, es tomar una medición basal de referencia y una o varias mediciones en distintos momentos posteriores de seguimiento. Después, podemos observar la diferencia de dichas mediciones posteriores con la situación basal, para ver si ha habido un cambio en dicha variable. Sin embargo, a que se debe dicho cambio, pudiendo ser a un efecto de la intervención aplicada, historia natural, errores en el procedimiento de medición, etc. También puede deberse a una combinación de estos, influyendo algunos más y otros menos, por ejemplo:
Para poder saber cuál es la efectividad de la intervención, si es que hay
alguna, debemos poder restar a dicha mejoría observada el efecto atribuible a
otros factores, como los errores de medición o la historia natural. Sin
embargo, esto no puede realizarse con un solo grupo de sujetos, ya que no
tenemos forma de saber cuánto ha influido cada factor, por ello es necesario
contar con un grupo no expuesto a la intervención, pero si a los otros factores
que pueden influir en que los pacientes cambien a lo largo del tiempo. Esto es
lo que se realiza en un ensayo clínico aleatorizado. Por ejemplo, podemos
comparar un programa de ejercicio (grupo experimental) con un grupo que no
reciba tratamiento (grupo control). La mejoría del grupo de ejercicio podría
ser la siguiente:
Como se ha comentado, no sabemos cuándo ha contribuido cada factor a dicha mejoría y si hay o no algún efecto del tratamiento. La mejoría del grupo control podría ser esta:
Dado que lo único que diferencia (si se ha realizado bien el estudio) al grupo experimental del control, es la aplicación de ejercicio terapéutico, si calculamos la diferencia entre ambos podremos obtener una estimación del efecto de la intervención:

Diferencias intra-grupo dentro del contexto de un ensayo clínico aleatorizado
Como se ha comentado, las diferencias intra-grupo no nos aportan información sobre la efectividad de una intervención, siendo esta información aportada por las diferencias entre-grupos. Entonces, ¿Qué utilidad tienen las diferencias intra-grupo en un ensayo aleatorizado?
Utilidad de la medición basal (antes de la intervención)
En contra de la intuición, las mediciones basales, antes de aplicar el tratamiento, no son en absoluto necesarias para poder evaluar la efectividad de una intervención en un ensayo aleatorizado. Se puede realizar un estudio aleatorizado midiendo solo a los 3 meses de haber aplicado la intervención, y poder obtener estimaciones precisas de la efectividad de esta.
Volviendo a la práctica clínica, si tenemos dos sujetos, uno que con una intensidad de dolor post-tratamiento de 3 y otro de 2.9 podríamos pensar que ambos han mejorado por igual, sin embargo, nos faltaría un dato, la situación de dolor basal de la que partían. Si uno de los sujetos partía de una intensidad de 8 y el otro de 4, las mejorías de uno y otro serían 5 y 2.1, habiendo claras diferencias (aunque no sabríamos si la mejoría sería por el tratamiento). Es decir, el calcular el cambio intra-grupo, con respecto a la medición basal, es una forma de “ajustar” o “controlar” para posibles diferencias en la situación basal, ya que la diferencia de los sujetos en el post-tratamiento depende de sus diferencias en la situación basal, y sin tener en cuenta la misma entonces podríamos malinterpretar quien ha mejorado más o menos.
En un ensayo aleatorizado, ese control de la situación basal se realiza mediante el proceso de asignación aleatoria a los grupos de tratamiento, que hace que la asignación al tratamiento sea independiente de la situación basal de los sujetos en la variable de interés y en todas las variables confusoras (medidas o sin medir en el estudio). Por ello, en este tipo de diseños no sería necesario como se ha comentado una medición basal para poder analizar la efectividad de un determinado tratamiento, pudiéndose analizar simplemente las diferencias post-tratamiento entre los grupos.
El motivo por el cual se realiza una medición basal, antes de aplicar la intervención, es porque de esta forma podemos mejorar la potencia estadística, siendo más fácil encontrar un efecto de la intervención bajo estudio, si es que existe alguno. Es decir, se realiza para disminuir el número de sujetos necesarios para llevar a cabo la investigación.
Cuando se dice que la aleatorización hace que la asignación al tratamiento sea independiente de la situación basal, implica decir que la diferencia media esperada (“real”) entre los grupos en la situación basal es de cero. Se habla de diferencia media esperada porque es el valor al que tiende dicho estadístico cuando el tamaño muestral tiende a infinito, sin embargo, en investigación las muestras nunca suelen ser tan grandes y, por tanto, siempre se observan pequeñas diferencias en la situación basal entre los grupos, originadas por la asignación aleatoria. Como sabemos que la diferencia real es de cero, si medimos la situación basal (previa al tratamiento), podemos incluir esa variable en un tipo de análisis conocido como Análisis de la Covarianza, para forzar a que dicha diferencia será cero en la situación basal en nuestro estudio, ajustándose las diferencias post-tratamiento y la precisión en la estimación de estas, mejorando la potencia estadística de los ensayos clínicos y, por tanto, necesitándose menos muestra.
Los cambios como un modelo de regresión
Cuando calculamos la diferencia en dos momentos de tiempo de una variable, el objetivo es “ajustar” o “controlar” para la situación basal. En la práctica clínica normalmente medimos a un paciente varias veces, de modo que solo podemos realizar esta resta. Sin embargo, en una investigación se suele medir a un conjunto de pacientes (una muestra), siendo este procedimiento de resta simple inadecuado.
Desde un punto de vista de un modelo de regresión lineal, la medición post-tratamiento (Ypost) puede definirse como:
$$Y_{post} = C + b_1*Y_{basal} + error$$
Cuando calculamos manualmente la diferencia (post- menos basal) de cada sujeto, estamos asumiendo el siguiente modelo:
$$Y_{post} – Y_{basal} = C + error$$
La única forma de que las dos ecuaciones se igualen, es que b1 (el coeficiente de regresión sin estandarizar) sea igual a 1, algo que rara vez sucede en la práctica. Dado que el objetivo de calcular el cambio post- menos basal es “controlar” para discrepancias en la situación basal, eso implica que la variable “Diferencia” obtenida, debe ser independiente de la situación basal (correlación = 0), algo que solo sucederá si b1 = 1. De no ser así, habrá una relación entre la diferencia y la situación basal, como se muestra a continuación con datos simulados:
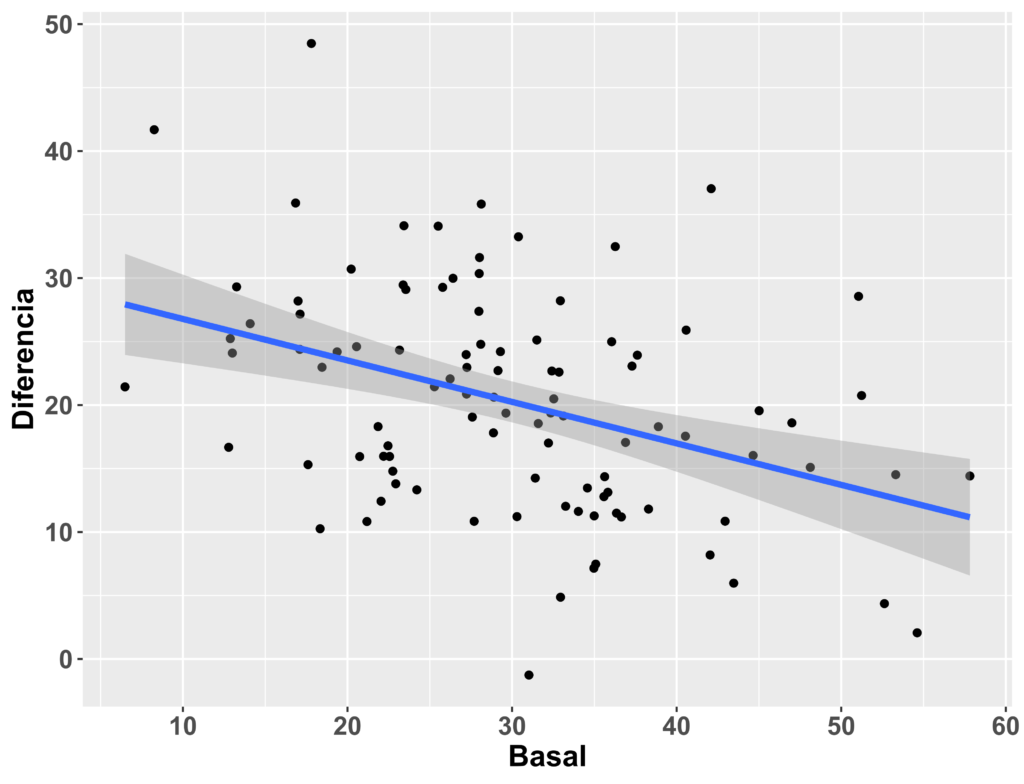
Esto tiene dos implicaciones. Por un lado, sigue habiendo dependencia con la situación basal, pudiéndose sobreestimar o infraestimar el posible efecto de la intervención, y por otro, no se minimizarían los errores del modelo de regresión, disminuyendo por tanto la precisión y potencia estadística del estudio.
Los ensayos aleatorizados como un modelo de regresión
Partamos ahora del contexto de un ensayo aleatorizado, donde se van a comparar dos grupos, uno que recibe un tratamiento experimental y un grupo control sin tratamiento, tomándose mediciones en la situación basal y a los 6 meses de seguimiento. En este caso tenemos tres posibilidades para comparar ambos grupos: ver las diferencias en el post-tratamiento, calcular el cambio del post- con respecto a la medición basal y ver las diferencias entre los grupos en esta nueva variable, o utilizar un análisis de la covarianza. El modelo de regresión de cada una de estas opciones sería:
Comparar POST-
$$Y_{post} = C + b_1*Tratamiento$$
Comparar CAMBIO
$$Y_{post} – Y_{basal} = C + b_1*Tratamiento$$
Modelo ANCOVA
$$Y_{post} = C + b_1*Tratamiento + b_2*Y_{basal}$$
En el primer caso (POST-), se asume que la relación entre la medición post-tratamiento y la medición basal es de cero (b2 = 0); en el segundo caso, como se comentaba en el apartado anterior, se asume que b2 es igual a 1; y finalmente en el tercer caso, se deja al modelo de regresión calcular la mejor estimación posible de b2, en lugar de asumir un valor concreto, para minimizar los errores del modelo. En los tres casos, el coeficiente b1 sería la diferencia media entre ambos grupos.
Como se comentaba al inicio de la entrada, no es necesario tomar mediciones basales para poder evaluar la efectividad de una intervención en un ensayo aleatorizado, siendo también innecesario el cálculo de la diferencia con respecto a la medición basal, teniendo estos procedimientos simplemente la utilidad de mejorar la potencia estadística y precisión (cuando la correlación entre la medición post- y la basal no es igual a cero). En otras palabras, si la muestra es lo suficientemente grande, dará igual que evaluemos solo las diferencias post-tratamiento, ya que la asignación aleatoria asegura una diferencia basal nula cuando la muestra tiende a infinito. Por ejemplo, asumiendo una diferencia media de 0.5 y una desviación estándar de 1, la muestra necesaria para una potencia deseada del 90%, en función de la correlación entre la medición basal y la post-tratamiento, para cada uno de los tres modelos sería:

Como se puede apreciar en el gráfico, el modelo de ANCOVA optimiza la disminución de los errores del modelo, requiriéndose siempre menos muestra salvo que la correlación sea de 0 o de 1, donde tendría la misma utilidad que el modelo POST-tratamiento o el modelo CAMBIO, pero no menos utilidad. Dado que la potencia estadística solo puede ir de 0 a 100, si incrementásemos mucho el tamaño muestral (ej. 10,000 sujetos por grupo) daría igual que modelo utilizásemos en un ECA, ya que la potencia tendería a su limite superior de 100, siendo las diferencias entre los 3 métodos irrelevantes. Sin embargo, esta no suele ser la situación habitual en la práctica, donde al haber menos muestra, se pueden observar pequeñas diferencias a nivel basal entre los grupos, siendo recomendable por tanto el uso del ANCOVA que minimizaría los errores del modelo con respecto a los otros dos.
Centrándonos ahora en los coeficientes b1 de los tres modelos, es decir, en las diferencias medias entre los grupos, también se observa algo contraintuitivo. Tendemos a pensar que es algo distinto calcular las diferencias entre grupos del cambio con respecto a la medición basal, a calcular las diferencias solo en el post-tratamiento, o mediante el uso del ANCOVA, sin embargo, todos esos procedimientos están estimando lo mismo, el efecto de la intervención, es decir, si incrementamos la muestra lo suficiente, los coeficientes b1 de cada uno de los 3 modelos tenderán todos hacia un mismo valor, estiman lo mismo. Lo único distinto es que cambia la precisión de la estimación y por eso se obtienen pequeñas diferencias de dichos coeficientes en un ensayo clínico realizado, pero a nivel conceptual son lo mismo. Por tanto, la creencia popular de que calcular el cambio con respecto a la situación basal para comparar dicha variable entre dos tratamientos, ofrece una visión más “real” de la efectividad de una intervención, porque estamos comparando mejorías en el tiempo, no se sostiene.
Los engaños de las diferencias intra-grupo en los ensayos aleatorizados
Como se explicaba al inicio del texto, la asignación aleatoria a los grupos de tratamiento es lo que garantiza la independencia con respecto a variables confusoras, de forma que la inferencia causal solo es aplicable en un ensayo aleatorizado a las diferencias entre-grupos, pero no a las intra-grupo. A pesar de ello, actualmente la mayoría de las revistas científicas de nuestro campo solicitan reportar las diferencias intra-grupo dentro del contexto de un ensayo clínico, un procedimiento que más que ayudar a interpretar mejor los resultados, solo puede confundir y sesgar más al lector, induciendo a malinterpretaciones del ensayo clínico. Por ejemplo, dado que la asignación aleatoria no elimina factores de confusión de las diferencias intra-grupo, donde también influyen aspectos como la historia natural, esto hace que dicha diferencia dentro del grupo experimental tienda a sobreestimar la efectividad de la intervención, ya que en ella también se sumaria el efecto de la historia natural del proceso en cuestión.
A continuación, muestro algunas preguntas frecuentes con sus respectivas respuestas, a fin de prevenir al lector tales malinterpretaciones (algunos aspectos ya se han comentado previamente):
Preguntas y respuestas
Si un grupo experimental mejora de manera significativa y el control no, ¿implica que la intervención es efectiva? | No |
Si dos grupos experimentales mejoran igual a lo largo del tiempo, ¿significa que ambas intervenciones son igual de efectivas, o que son efectivas? | No |
¿Es necesario tomar una medición basal (antes de aplicar el tratamiento) en un ensayo aleatorizado para evaluar la efectividad de este? | No |
Si las diferencias entre grupos no son significativas ni relevantes, pero solo el grupo experimental ha mostrado diferencias significativas intra-grupo, ¿significa que puede que la intervención sea efectiva? | No |
¿Calcular la diferencia post- menos basal en un ensayo aleatorizado es un procedimiento estadístico adecuado? | No |
¿Las diferencias intra-grupo sobreestiman el efecto de la intervención? | Si |
¿Son distintas a nivel conceptual las diferencias entre-grupos ajustadas de un ANCOVA y las calculadas mediante la variable diferencia post- menos basal? | No |
¿Es necesario observar las diferencias intra-grupo para interpretar adecuadamente los resultados de un ensayo aleatorizado? | No |
Literatura de interés
El tema tratado en esta entrada es complejo y con muchos matices y aspectos a tener en consideración, algunos no abordados en la misma. Por ello, recomiendo a cualquier persona interesada en la interpretación y realización de ensayos aleatorizados leer estas fuentes de información a fin de mejorar su entendimiento en esta materia:
- Analysing controlled trials with baseline and follow up measurements
- Best (but oft forgotten) practices: testing for treatment effects in randomized trials by separate analyses of changes from baseline in each group is a misleading approach
- What’s Wrong with Change in General? | BIOSTATISTICS FOR BIOMEDICAL RESEARCH (Libro de Frank E. Harrell Jr)
- The use of percentage change from baseline as an outcome in a controlled trial is statistically inefficient: a simulation study
- Explorations in statistics: the analysis of change
Conclusiones
Las diferencias intra-grupo no son necesarias dentro del contexto de un ensayo aleatorizado, pudiendo derivar solo en malinterpretaciones de los resultados del mismo. Por ello, es recomendable no tener en cuenta tales diferencias, incluso no reportarlas, cuando se lea o se realice un estudio con este tipo de diseño. Todo ensayo aleatorizado debería analizarse y reportarse con un modelo ANCOVA (u otra variante de modelo de regresión multivariable, incluyendo la medición basal como covariable).
Asunciones: Normalidad En esta entrada se recoge una breve explicación de la tan aclamada asunción de normalidad, haciendo hincapié en a que …
Análisis de la "normalidad": Gráficos QQ y PP En esta entrada se recoge una explicación de los gráficos QQ y PP, útiles …
Interpretación de la relevancia clínica: El mal uso de la mínima diferencia clínicamente relevante (I) En esta entrada se proporciona una breve …
Calculadora Muestral: Ensayos Aleatorizados (diferencia ajustada ancova – precisión) En esta entrada se recoge una breve guía práctica de recomendaciones para calcular …









