mínimos cuadrados ordinarios: definición simple
Los mínimos cuadrados ordinarios es un método de estimación de parámetros poblacionales mediante el modelo lineal, que se basa en minimizar el error cuadrático medio.
El método de mínimos cuadrados ordinarios es en el que se basan todos los análisis englobados dentro del modelo lineal general (t-Student, regresión lineal simple y múltiple, Análisis de la Varianza…). Este método consiste en minimizar la suma de cuadrados del error de predicción del modelo, que tiene sentido cuando se cumplen una serie de asunciones, que son las necesarias para poder realizar ese tipo de análisis. Dado que el concepto de media como estimador se basa también en este método, lo explicaré con ella, pues facilita la comprensión del mismo.
Imaginemos que tenemos la siguiente muestra de 9 sujetos, a los cuales medimos el peso:
$$ x = \{64, 65, 66, 67, 68, 69, 70, 71, 72\}$$
Ahora, queremos usar algún valor comprendido entre 64 y 72 como predictor de todos los sujetos. Al hacerlo, cometeremos errores, ya que habrá una diferencia entre el valor real de cada sujeto y el valor que hemos utilizado como predictor, de modo que podemos calcular la suma de cuadrados (SS) como estimador del error de predicción para distintos valores, que vamos a suponer como si fuesen «medias», cuyo valor seleccionamos nosotros a nuestro antojo y no con la fórmula descrita para la media, por ejemplo:
$$\bar x = 64 \rightarrow SS = 204$$
$$\bar x = 71 \rightarrow SS = 141$$
$$\bar x = 62 \rightarrow SS = 384$$
$$\bar x = 70 \rightarrow SS = 96$$
Podemos hacer esto para el conjunto de valores entre el mínimo (64) y el máximo (72) de la muestra, obteniendo el siguiente gráfico:
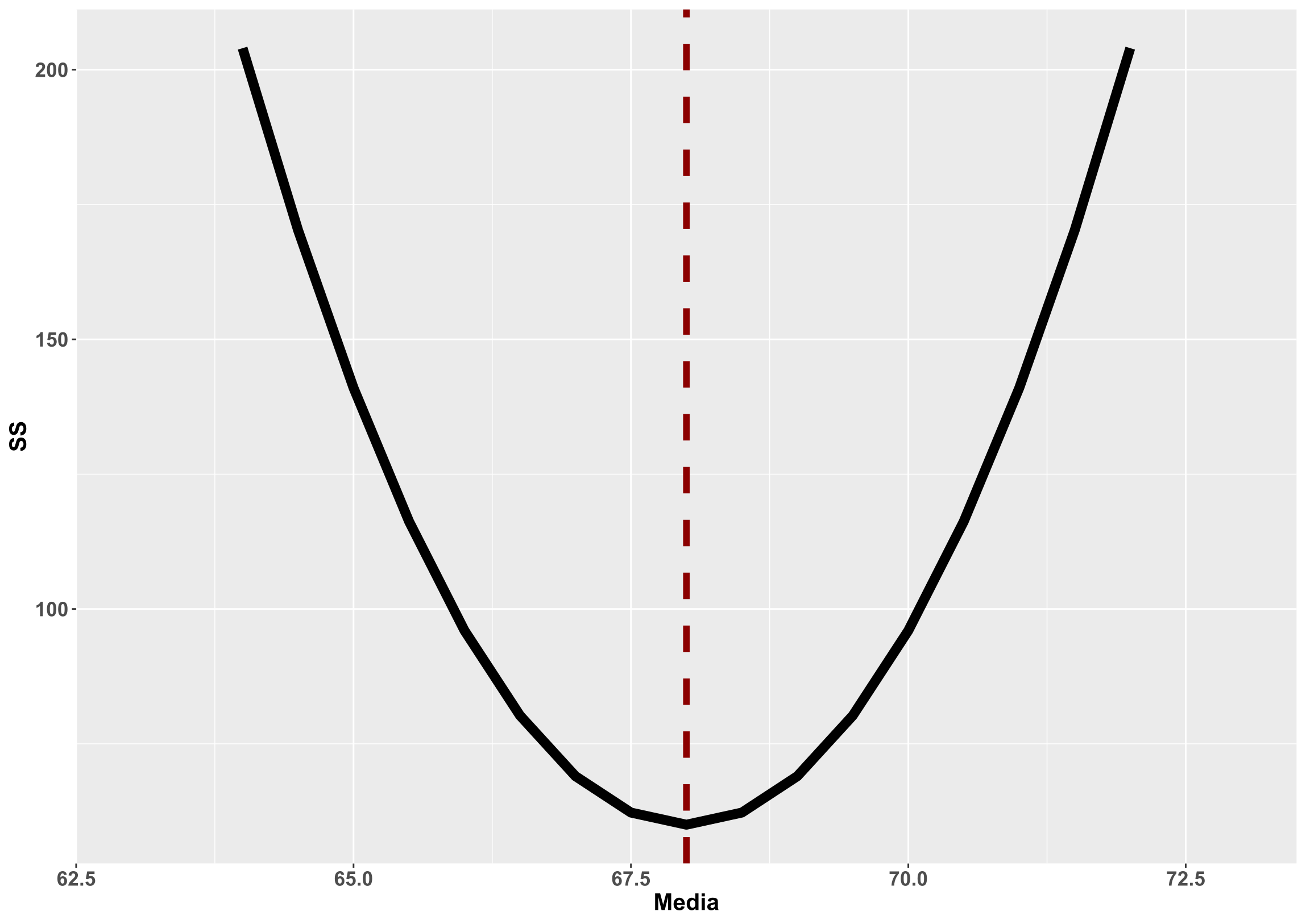
Como se puede apreciar, la representación gráfica de la suma de cuadrados (eje y) y el valor usado de la media (eje x) para calcular dicha suma de cuadrados, da lugar a una parábola. El vértice de la misma es el punto donde la suma de cuadrados es mínima y coincide con el valor de la media calculada con la fórmula mostrada en su respectiva entrada (marcada en el gráfico con una línea roja discontinua vertical). Queda por tanto demostrado que el uso de la media calculada con la fórmula descrita, para predecir los valores de una muestra, disminuye la suma de cuadrados de error, que es en lo que se basa el método de mínimos cuadrados ordinarios. En el resto de análisis, aunque de una manera quizás algo menos visual y más complicada de entender, se lleva a cabo el mismo procedimiento, por ejemplo, en una regresión lineal, se estiman los coeficientes de regresión para que dicha suma de cuadrados sea mínima.
Asunciones: Normalidad En esta entrada se recoge una breve explicación de la tan aclamada asunción de normalidad, haciendo hincapié en a que …
Análisis de la "normalidad": Gráficos QQ y PP En esta entrada se recoge una explicación de los gráficos QQ y PP, útiles …
Interpretación de la relevancia clínica: El mal uso de la mínima diferencia clínicamente relevante (I) En esta entrada se proporciona una breve …
Calculadora Muestral: Ensayos Aleatorizados (diferencia ajustada ancova – precisión) En esta entrada se recoge una breve guía práctica de recomendaciones para calcular …




